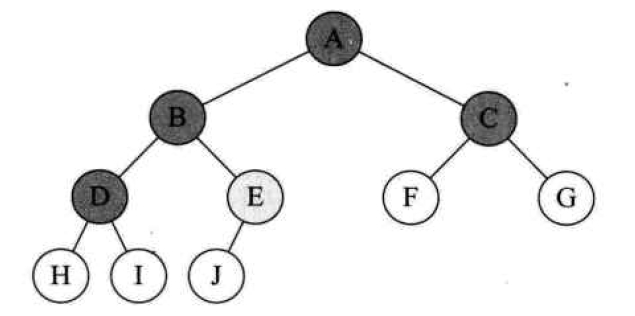
经过几天的学习,简单的编写了一个二叉树的类
其中包括
属性
- 根节点
方法
- 层序构建二叉树
- 前序构建二叉树
- 得到当前的深度
- 得到当前的节点数
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
//
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Stack;
public class BinaryTree {
/**
* 根节点
*/
public TreeEntry root;
/**
* 构造函数初始化根节点
* @param rootData
*/
public BinaryTree(T rootData) {
root = new TreeEntry(1, rootData);
}
/**
* 构造函数初始化根节点
*/
public BinaryTree() {
}
/**
* 根据层序构建二叉树
* @param a 可选参数
*/
public void newBinaryTreeByIndex(T... a) {
if (root == null) {
root = new TreeEntry(1, a[0]);
a = Arrays.copyOfRange(a, 1, a.length);
}
TreeEntry buffer = root;
// 通过队列构造二叉树
LinkedList child = new LinkedList();
// 将根节点插入队列
child.offer(buffer);
// 第一个节点的序号为2
int i = 2;
// 遍历可选参数
for (T data : a) {
// 根据当前序号选择左孩子还是右孩子
switch (i % 2) {
// 可以被2整除为做孩子
case 0:
// 取出父节点
buffer = child.peek();
// 通过当前序号和数据构建节点,并设置为父节点的左孩子
buffer.leftChild = new TreeEntry(i, data);
// 将左孩子插入到队列
child.offer(buffer.leftChild);
break;
// 除2余1为右孩子
case 1:
// 取出父节点,并移除父节点(弹出)
// 因为二叉树每个节点只有两个孩子节点,所以当添加右孩子节点以后可以移除
buffer = child.poll();
// 通过当前序号和数据构建节点,并设置为父节点的右孩子
buffer.rightChild = new TreeEntry(i, data);
// 将右孩子插入到队列
child.offer(buffer.rightChild);
break;
default:
new RuntimeException("构建二叉树错误!");
break;
}
// 自增序号
i++;
}
}
/**
* 根据前序构建二叉树
* @param a 可选参数
*/
public void newBinaryTreeByPrePrder(T... a) {
// 创建线性表
ArrayList list = new ArrayList();
// 将数组数据复制到线性表
Collections.addAll(list, a);
putByPreOrder(1, list);
}
/**
* 前序添加二叉树
* @param index 序号
* @param list 剩余元素
* @return 二树
*/
public TreeEntry putByPreOrder(int index, ArrayList list) {
// 取出元素
T element = list.get(0);
// 如果元素为空则移除元素返回
if (element == null) {
list.remove(0);
return null;
}
// 创建新节点
TreeEntry buffer = new TreeEntry(index, element);
// 如果没有跟元素,则设置为根元素
if (root == null) {
root = buffer;
}
// 移除该元素
list.remove(0);
// 通过迭代创建子树
buffer.leftChild = putByPreOrder(index++, list);
buffer.rightChild = putByPreOrder(index++, list);
// 返回子树
return buffer;
}
/**
* 得到当前树的深度
* @return 深度
*/
public int getHeight() {
return getHeright(root);
}
/**
* 递归二叉树深度私有方法
* @param tree 父节点
* @return 深度
*/
private int getHeright(TreeEntry tree) {
// 如果父节点点为空,则返回0
if (tree == null) {
return 0;
} else {
// i为左子树的深度,j为右子树的深度
int i = 0, j = 0;
// 递归得到左子树的深度
i = getHeright(tree.leftChild);
// 递归的得到右子树的深度
j = getHeright(tree.rightChild);
// 返回左右子树深度更深的一个并加当前层数
return i >= j ? i + 1 : j + 1;
}
}
/**
* 得到当前树的节点数
* @return
*/
public int getSize() {
return getSize(root);
}
/**
* 递归二叉树节点数方法
* @param tree 父节点
* @return 节点数
*/
private int getSize(TreeEntry tree) {
// 如果节点为空,则返回0
if (tree == null) {
return 0;
} else {
// i为左子树的节点数,j为右子树的节点数
int i = 0, j = 0;
// 递归得到左子树节点数
i = getSize(tree.leftChild);
// 递归得到右子树节点数
j = getSize(tree.rightChild);
// 返回子树节点数并加当前节点
return i + j + 1;
}
}
/**
* 递归前序遍历当前树
*/
public void preOrder() {
preOrder(root);
}
/**
* 递归二叉树前序遍历方法
* @param tree
*/
private void preOrder(TreeEntry tree) {
// 如果为空则返回
if (tree == null) {
return;
} else {
// 前序遍历的顺序为,根左右
// 输出根的数据
System.out.println(tree.data);
// 前序遍历左子树
preOrder(tree.leftChild);
// 前序遍历右子树
preOrder(tree.rightChild);
}
}
/**
* 非递归前序遍历当前树
*/
public void nonRecPreOrder() {
nonRecPreOrder(root);
}
/**
* 非递归二叉树前序遍历方法
* @param tree
*/
private void nonRecPreOrder(TreeEntry tree) {
// 通过栈遍历二叉树
Stack child = new Stack();
// 将根节点压如栈中
child.push(tree);
// 构建临时引用变量
TreeEntry temp;
// 前序遍历的顺序为,根左右
// 如果栈不为空则循环
while (!child.isEmpty()) {
// 将栈顶元素弹出到临时变量
temp = child.pop();
// 输出根元素
System.out.println(temp.data);
// 因为栈是后入先出,所以要想先遍历左孩子节点,就要先插入右孩子节点
if (temp.rightChild != null) {
// 将右孩子节点压入栈中
child.push(temp.rightChild);
}
if (temp.leftChild != null) {
// 将左孩子节点压入栈中
child.push(temp.leftChild);
}
}
}
/**
* 递归中序遍历当前树
*/
public void midOrder() {
midOrder(root);
}
/**
* 递归二叉树中序遍历方法
* @param tree
*/
private void midOrder(TreeEntry tree) {
// 如果节点为空,则返回
if (tree == null) {
return;
} else {
// 中序遍历的顺序为,左根右
// 中序遍历左子树
midOrder(tree.leftChild);
// 输出根节点
System.out.println(tree.data);
// 中序遍历右子树
midOrder(tree.rightChild);
}
}
/**
* 非递归中序遍历当前树
*/
public void nonRecMidOrder() {
nonRecMidOrder(root);
}
/**
* 非递归二叉树中序遍历方法
* @param tree
*/
private void nonRecMidOrder(TreeEntry tree) {
// 通过栈遍历二叉树
Stack child = new Stack();
// 构建临时引用变量
TreeEntry temp = tree;
// 中序遍历顺序,左根右
// 如果临时变量不为空 或 栈不为空则循环
while (temp != null || !child.isEmpty()) {
// 遍历节点,将当前节点的左孩子节点压入栈中,直到没有左孩子节点为止
// 如果临时变量不为空则循环
while (temp != null) {
// 将当前遍历压入栈中
child.push(temp);
// 将临时变量设置为左孩子节点
temp = temp.leftChild;
}
// 遍历每个节点的右孩子节点
// 如果栈不为空
if (!child.isEmpty()) {
// 将栈顶元素弹出到临时变量
temp = child.pop();
// 输出当前节点的数据
System.out.println(temp.data);
// 将临时变量设置为右孩子节点,使循环后右孩子节点进行遍历左孩子节点
temp = temp.rightChild;
}
}
}
/**
* 递归后序遍历当前树
*/
public void postOrder() {
postOrder(root);
}
/**
* 递归二叉树后续遍历方法
* @param tree
*/
private void postOrder(TreeEntry tree) {
// 如果当前节点为空则返回
if (tree == null) {
return;
} else {
// 后续遍历的顺序为,左右根
// 后续遍历左子树
postOrder(tree.leftChild);
// 后续遍历右子树
postOrder(tree.rightChild);
// 输出根元素
System.out.println(tree.data);
}
}
/**
* 非递归后续遍历当前树
*/
public void nonRecPostOrder() {
nonRecPostOrder(root);
}
/**
* 非递归二叉树后续遍历
* @param tree
*/
private void nonRecPostOrder(TreeEntry tree) {
// 通过栈后序遍历二叉树
Stack child = new Stack();
// 创建临时节点 和 上一个遍历的节点,并赋值为根节点
TreeEntry temp = tree, prev = tree;
// 如果临时节点不为空 或 栈不为空则继续遍历则循环
while (temp != null || !child.isEmpty()) {
// 遍历节点,将当前节点的左孩子节点压入栈中,直到没有左孩子节点为止
// 如果临时变量不为空则循环
while (temp != null) {
child.push(temp);
temp = temp.leftChild;
}
// 遍历每个节点的右孩子节点
// 如果栈不为空
if (!child.isEmpty()) {
// 取出栈顶元素的右孩子节点设置为临时右孩子节点
TreeEntry tempRight = child.peek().rightChild;
// 如果临时右孩子节点为空,或者临时右孩子节点是上一个遍历的节点,则遍历父节点
// 否则,临时右孩子节点不为空,遍历临时右孩子节点的子树
if (tempRight == null || tempRight == prev) {
// 弹出栈顶元素(临时右孩子节点的父节点),并设置为临时节点
temp = child.pop();
// 输出临时节点的数据
System.out.println(temp.data);
// 将临时节点设置为上一个遍历的节点
prev = temp;
// 将临时节点设置为空
temp = null;
} else {
// 将临时右孩子节点设置为临时节点,进入下一个循环时,遍历临时右孩子节点的子树
temp = tempRight;
}
}
}
}
/**
* 递归层序遍历当前树
*/
public void indOrder() {
indOrder(root);
}
/**
* 递归二叉树层序遍历方法
* @param tree
*/
private void indOrder(TreeEntry tree) {
// 如果当前节点为空,则返回
if (tree == null) {
return;
} else {
// 通过队列进行层序宾利
LinkedList child = new LinkedList();
// 将根节点存入队列
child.offer(tree);
// 设置临时节点变量
TreeEntry temp;
// 输出当前节点
System.out.println(tree.data);
// 如归队首节点不为空,则循环
while ((temp = child.poll()) != null) {
// 如果临时节点的左孩子节点不为空
if (temp.leftChild != null) {
// 输出左孩子节点的数据
System.out.println(temp.leftChild.data);
// 将左孩子节点存入队列
child.offer(temp.leftChild);
}
// 如果临时节点的右孩子节点不为空
if (temp.rightChild != null) {
// 输出右孩子节点的数据
System.out.println(temp.rightChild.data);
// 将右孩子节点的存入队列
child.offer(temp.rightChild);
}
}
}
}
public class TreeEntry {
private int index;
private T data;
private TreeEntry leftChild;
private TreeEntry rightChild;
public TreeEntry(int index) {
super();
this.index = index;
}
public TreeEntry(int index, T data) {
super();
this.index = index;
this.data = data;
}
public int getIndex() {
return index;
}
public void setIndex(int index) {
this.index = index;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public TreeEntry getLeftChild() {
return leftChild;
}
public void setLeftChild(TreeEntry leftChild) {
this.leftChild = leftChild;
}
public TreeEntry getRightChild() {
return rightChild;
}
public void setRightChild(TreeEntry rightChild) {
this.rightChild = rightChild;
}
@Override
public String toString() {
return data.toString();
}
}
}

