-
算法准备
a. Edge度对象数组(从小到大)
b. 查询数组parent
c. find方法(查找数组中该顶点能到达的最后位置)
-
算法思路
a. 遍历edge数组
b. 通过find方法取得edge对象头顶点的最后下标
c. 通过find方法取得edge对象尾顶点的最后下标
d. 如果头尾下标不相等
e. 输出度的信息
f. 将parent数组中头下标位置的值设置为尾下标
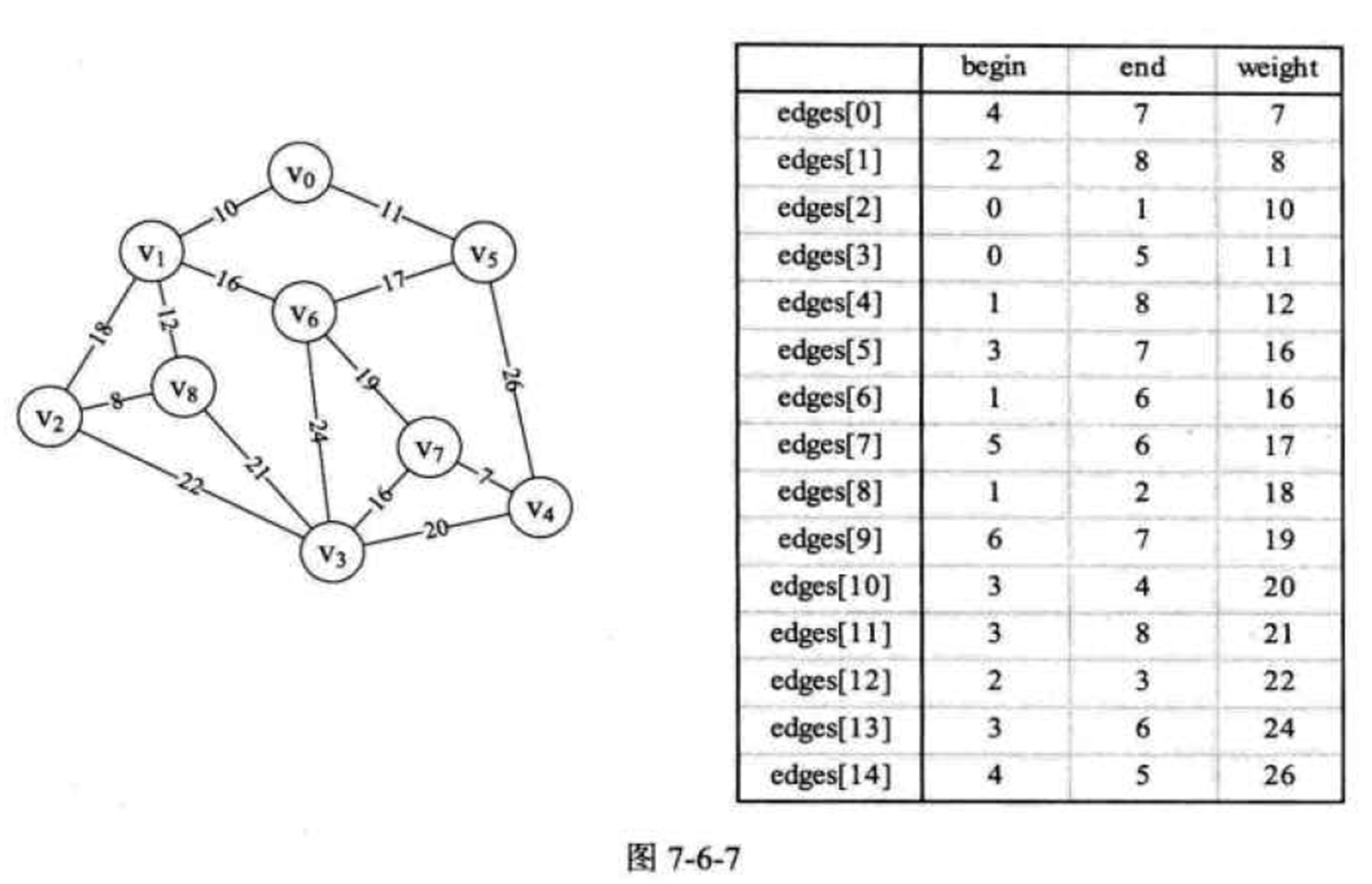
//
public class Graph<T extends Comparable<T>> {
// 顶点数组
private T[] vertexs;
// 邻接表元素数组
private VertexNeighborNode<T>[] neighborArray;
// 邻接矩阵
private int[][] matrix;
// 度数组
private Edge[] edges;
// 泛型对象的类文件
private Class<T> Class;
// 顶点数量
private int size;
// 常亮:未连接
public static final int NO_LINK = -1;
/**
* 最小生成树方法-克鲁斯卡尔算法
*/
public void kruskal() {
// 创建查找数组
// 该数组下标为顶点下边
// 该数组值为顶点出度顶点下标
int[] parent = new int[size];
// 最小权值和
int sum = 0;
// 构建度数组
createEdge();
// 循环出度数组
for (Edge edge : edges) {
// 从查找数组中寻找该出度的头所到达的顶点下标
int n = find(parent, edge.begin);
// 从查找数组中寻找该出度的尾所到达的顶点下标
int m = find(parent, edge.end);
// 如果头尾顶点下标不相等,进入
// 如果头尾顶点下标相对,则代表该度为多余度
if (n != m) {
// 输出该度信息
System.out.println(
edge.begin + "顶点---" + edge.end + "顶点:" + edge.weight);
// 将查询数组中头下标的值设置为尾下标
parent[n] = m;
// 累计权值
sum += edge.weight;
}
}
// 输出权值
System.out.println(sum);
}
/**
* 查找数组中该顶点能到达的最后位置
* @param parent 查找数组
* @param i 顶点下标
* @return 最后位置
*/
private int find(int[] parent, int i) {
// 如果该下标位置有出度则循环
while (parent[i] > 0) {
// 将出度下标设置为下一次查找的下标
i = parent[i];
}
// 返回最后位置
return i;
}
* 构建度数组
*/
public void createEdge() {
// 创建度的链表,不确定度的数量,所以使用链表
List<Edge> edgeList = new LinkedList<Edge>();
// 从第一个顶点开始构建度的链表
createEdge(edgeList, 0);
// 创建度的数组
this.edges = new Edge[edgeList.size()];
// 数组赋值标记
int i = 0;
// 遍历链表,添加到数组
for (Edge edge : edgeList) {
// 将链表值添加到数组
this.edges[i] = edge;
// 标记自增
i++;
}
// 通过Edge类实现Comparable接口进行排序
Arrays.sort(this.edges);
}
/**
* 构建度数组
*
* 此方法思路与广度优先相同
* 但是没有采用上面的递归广度优先思路
* 而是使用迭代完成
* @param edges 度的链表
* @param i 开始节点
*/
private void createEdge(List<Edge> edges, int i) {
// 创建度的队列
LinkedList<Integer> queue = new LinkedList<Integer>();
// 将顶点下标添加到队列中
queue.offer(i);
// 队列不为空则循环
while (!queue.isEmpty()) {
// 取出队首顶点下标
int n = queue.poll();
// 取得顶点的第一个邻接点
int m = getFirstNeighbor(n);
// 当邻接点连接时循环
while (m != NO_LINK) {
// 是否包含度标记
boolean isHave = false;
// 遍历度链表
for (Edge e : edges) {
// 如果两节点相等
if (e.equals(n, m, matrix[n][m])) {
// 将标记设置为真
isHave = true;
break;
}
}
// 当没有该度时
if (!isHave) {
// 向度链表中添加该度
edges.add(new Edge(n, m, matrix[n][m]));
// 将邻接点下标添加到队尾
queue.offer(m);
}
// 得到m邻接点后的一个邻接点
m = getNextNeighbor(n, m);
}
}
}
/**
*
* ClassNameCh 度
* ClassNameEn Edge
* Description 度的数据结构
* Company
* @author Naah
* @date 2017年8月14日 下午10:52:53
*/
class Edge implements Comparable<Edge> {
// 度的头顶点下标
int begin;
// 度的尾顶点下标
int end;
// 度的权值
int weight;
public Edge() {
super();
}
/**
* 构造函数
* @param begin 头顶点下标
* @param end 尾顶点下标
* @param weight 权值
*/
public Edge(int begin, int end, int weight) {
super();
this.begin = begin;
this.end = end;
this.weight = weight;
}
/**
* 判断相等方法
* @param begin
* @param end
* @param weight
* @return true/false
*/
public boolean equals(int begin, int end, int weight) {
// 首先判断权值相等
if (weight == this.weight) {
// 判断下标是否相同,包括头尾互换
if ((begin == this.begin && end == this.end)
|| (end == this.begin && begin == this.end)) {
// 返回相等
return true;
}
}
// 返回不相等
return false;
}
@Override
public String toString() {
return "Edge [begin=" + begin + ", end=" + end + ", weight=" + weight
+ "]";
}
/**
* 判断大小方法
* 以权值大小判断,为度数组的从小到大排序
*/
@Override
public int compareTo(Edge o) {
if (this.weight > o.weight) {
return 1;
} else if (this.weight < o.weight) {
return -1;
}
return 0;
}
}
* 构建度数组
*/
public void createEdge() {
// 创建度的链表,不确定度的数量,所以使用链表
List<Edge> edgeList = new LinkedList<Edge>();
// 从第一个顶点开始构建度的链表
createEdge(edgeList, 0);
// 创建度的数组
this.edges = new Edge[edgeList.size()];
// 数组赋值标记
int i = 0;
// 遍历链表,添加到数组
for (Edge edge : edgeList) {
// 将链表值添加到数组
this.edges[i] = edge;
// 标记自增
i++;
}
// 通过Edge类实现Comparable接口进行排序
Arrays.sort(this.edges);
}
/**
* 构建度数组
*
* 此方法思路与广度优先相同
* 但是没有采用上面的递归广度优先思路
* 而是使用迭代完成
* @param edges 度的链表
* @param i 开始节点
*/
private void createEdge(List<Edge> edges, int i) {
// 创建度的队列
LinkedList<Integer> queue = new LinkedList<Integer>();
// 将顶点下标添加到队列中
queue.offer(i);
// 队列不为空则循环
while (!queue.isEmpty()) {
// 取出队首顶点下标
int n = queue.poll();
// 取得顶点的第一个邻接点
int m = getFirstNeighbor(n);
// 当邻接点连接时循环
while (m != NO_LINK) {
// 是否包含度标记
boolean isHave = false;
// 遍历度链表
for (Edge e : edges) {
// 如果两节点相等
if (e.equals(n, m, matrix[n][m])) {
// 将标记设置为真
isHave = true;
break;
}
}
// 当没有该度时
if (!isHave) {
// 向度链表中添加该度
edges.add(new Edge(n, m, matrix[n][m]));
// 将邻接点下标添加到队尾
queue.offer(m);
}
// 得到m邻接点后的一个邻接点
m = getNextNeighbor(n, m);
}
}
}
/**
}
class Edge implements Comparable<Edge> {
// 度的头顶点下标
int begin;
// 度的尾顶点下标
int end;
// 度的权值
int weight;
public Edge() {
super();
}
/**
* 构造函数
* @param begin 头顶点下标
* @param end 尾顶点下标
* @param weight 权值
*/
public Edge(int begin, int end, int weight) {
super();
this.begin = begin;
this.end = end;
this.weight = weight;
}
/**
* 判断相等方法
* @param begin
* @param end
* @param weight
* @return true/false
*/
public boolean equals(int begin, int end, int weight) {
// 首先判断权值相等
if (weight == this.weight) {
// 判断下标是否相同,包括头尾互换
if ((begin == this.begin && end == this.end)
|| (end == this.begin && begin == this.end)) {
// 返回相等
return true;
}
}
// 返回不相等
return false;
}
@Override
public String toString() {
return "Edge [begin=" + begin + ", end=" + end + ", weight=" + weight
+ "]";
}
/**
* 判断大小方法
* 以权值大小判断,为度数组的从小到大排序
*/
@Override
public int compareTo(Edge o) {
if (this.weight > o.weight) {
return 1;
} else if (this.weight < o.weight) {
return -1;
}
return 0;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
}
