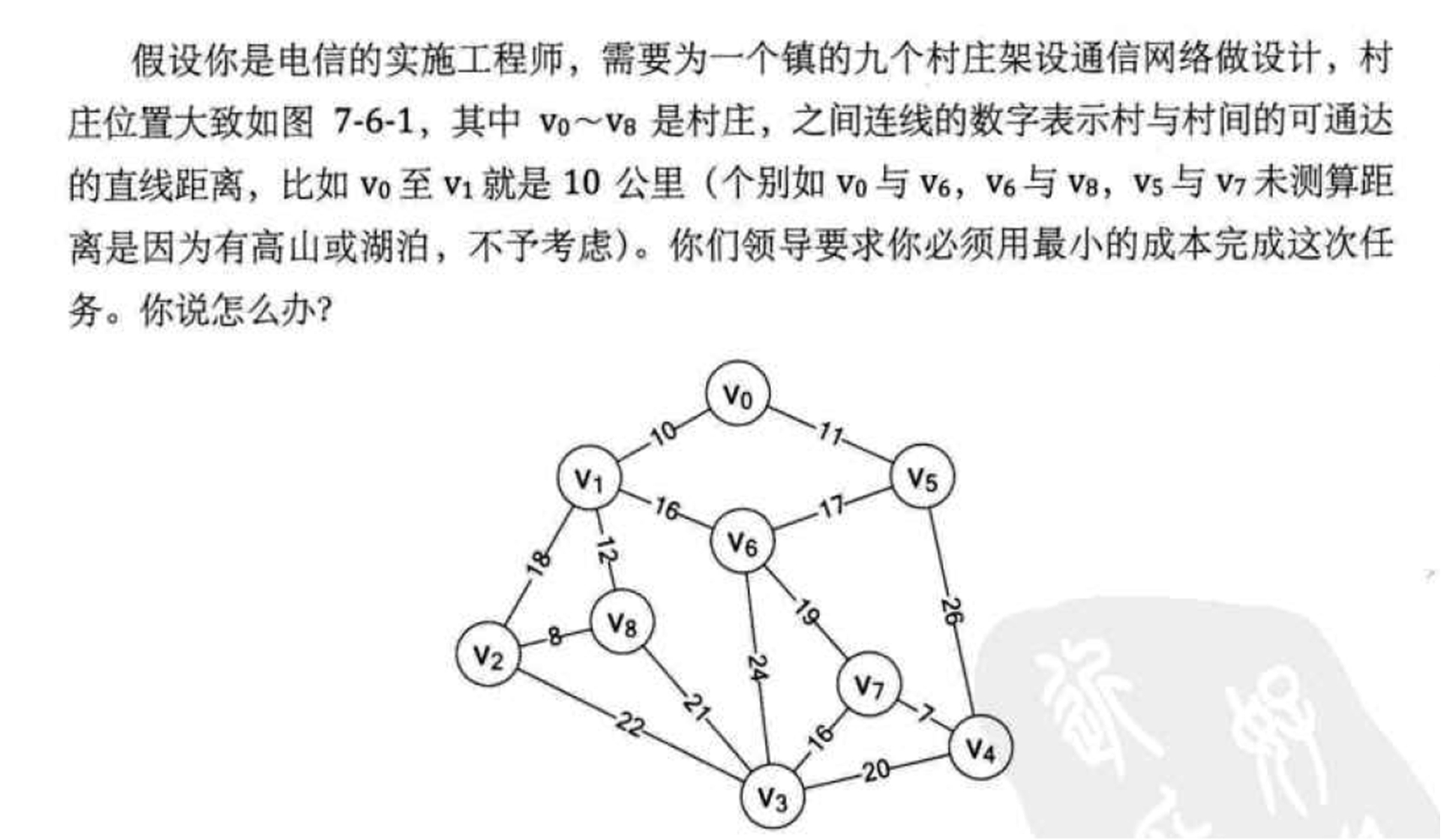
一个连通图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。我们把构造连通网的最小代价生成树。称为最小生成树
通过邻接矩阵进行计算
-
算法准备
a. 邻接矩阵
b. 最小权值数组least
c. 上一个顶点下标数组lastIndex
d. 最小权值和sum
-
算法思路
a. 将least数组初始化为邻接矩阵中第一个节点的出度数组
b. 开始循环
c. for循环least数组中最小的值,记录为min,并记录下标为minIndex
d. 输出度的信息,累加min到sum
e. for遍历minIndex数组中的权值
f. Least数组中该位置不为0(未遍历过)并且权值比least数组中小
g. 将该权值覆盖到least数组中的位置
h.设置lastIndex该位置为minIndex
public class Graph> {
// 顶点数组
private T[] vertexs;
// 邻接表元素数组
private VertexNeighborNode[] neighborArray;
// 邻接矩阵
private int[][] matrix;
// 泛型对象的类文件
private Class Class;
// 顶点数量
private int size;
// 常亮:未连接
public static final int NO_LINK = -1;
/**
* 构造方法
* @param Class 类对象
* @param vertexs 顶点可选数组
*/
public Graph(Class<T> Class, T... vertexs) {
super();
this.vertexs = vertexs;
this.size = vertexs.length;
this.Class = Class;
}
/**
* 构造方法
* @param vertexs 可选数组
*/
public Graph(T... vertexs) {
super();
this.vertexs = vertexs;
this.size = vertexs.length;
}
/**
* 得到邻接矩阵
* @return
*/
public int[][] getMatrix() {
return matrix;
}
/**
* 设置邻接矩阵
* @param matrix 邻接矩阵
* @throws Exception 数组长度不对
*/
public void setMatrix(int[][] matrix) throws Exception {
if (matrix.length != this.vertexs.length) {
throw new Exception("二维数组长度不对");
}
for (int i = 0; i < matrix.length; i++) {
if (matrix[i].length != this.vertexs.length) {
throw new Exception("二维数组长度不对");
}
}
this.matrix = matrix;
}
/**
* 最小生成树方法-普里姆算法
*
*/
public void prim() {
// 创建最小权值数组
int[] least = new int[size];
// 上一个顶点下标数组
int[] lastIndex = new int[size];
// 最小权值和
int sum = 0;
// 初始化最小权值数组
for (int i = 0; i < least.length; i++) {
least[i] = matrix[0][i];
}
// 循环查找最小生成树
for (int i = 1; i < least.length; i++) {
// 将最小权值设置为int最大值
int min = Integer.MAX_VALUE;
// 将最小权值下标设置为0
int minIndex = 0;
// 循环查找最小权值数组中的最小值
for (int j = 1; j < least.length; j++) {
// 大于0的最小权值
if (least[j] > 0 && least[j] < min) {
// 设置为最小值
min = least[j];
// 将当前下标设置为最小权值下标
minIndex = j;
}
}
// 输出已找到的最小顶点
System.out.println(
lastIndex[minIndex] + "顶点---" + minIndex + "顶点:" + min);
// 将已找到的最小权值点设置为0,标记为已找到
least[minIndex] = 0;
// 将最小权值累加到最小权值和中
sum += min;
// 将上一个顶点的所有出度权值添加到最小权值数组中
for (int j = 1; j < least.length; j++) {
// 没遍历的顶点 并且 上一个顶点所到该顶点的权值 小于 最小权值数组中到该顶点的权值时 进入
// 最小权值数组中无法到达的顶点 并且上一个顶点能到达该顶点时 进入
if ((least[j] > 0 && matrix[minIndex][j] != NO_LINK
&& matrix[minIndex][j] < least[j])
|| (least[j] == NO_LINK
&& matrix[minIndex][j] != NO_LINK)) {
// 将上一个顶点到该顶点的出度权值添加到最小权值数组中
least[j] = matrix[minIndex][j];
// 将上一个顶点设置为该顶点的入度顶点
lastIndex[j] = minIndex;
}
}
}
// 输出最小权值和
System.out.println(sum);
}
}
