1 概述
k-近邻算法采用测量不同特征值之间的距离的方法进行分类
2 优缺点
- 优点:精度高,对异常值不敏感,无数据输入假定
- 缺点:计算复杂度该,空间复杂度高,不能保存成模型
- 适用数据范围:数值型和标称型
3 数据准备
3.1 数据准备
- 要测试的向量。是我们要进行预测的数据
- 训练数据集,是不包含目标向量的特征数据集
- 标签组成的向量(目标变量组成的向量)
- k,就是我们所要查找的前多少个相似的,一般不大于20
3.2 数据整理
在上一篇文章我们讲到了归一化,不知道的小伙伴,快去看看吧!点我查看
下面提供一个较为简单的归一化公式:
new_value=(old_value-min)/(max-min)
old_value:原来的值
min:在数据集中该特征最小的值
max:在数据集中该特征最大的值
那我们看看如何用代码进行实现这个归一化吧!
import numpy
class Normalization(object):
def auto_norm(self, matrix):
"""
数据清洗,归一化
new_value=(old_value-min)/(max-min)
:param matrix: 矩阵
:return: 归一化的矩阵,范围数据,最小值
"""
# 0表示从列中选值
# 每列的最小值组成一个向量
min_value = matrix.min(0)
# 每列的最大值组成一个向量
max_value = matrix.max(0)
# 每列的范围值
ranges = max_value - min_value
m = matrix.shape[0]
norm_matrix = numpy.zeros(numpy.shape(matrix))
# 分子
norm_matrix = matrix - numpy.tile(min_value, (m, 1))
# 不是矩阵除法,矩阵除法是linalg.solve(matA,matB)
norm_matrix = norm_matrix / numpy.tile(ranges, (m, 1))
return norm_matrix, ranges, min_value
4 原理
4.1 算法思想
- 准备上方所说的数据
- 输入新数据后,将新数据复制成与训练数据集一样的矩阵,然后每条向量与训练数据集计算欧式距离
- 对计算出的欧式距离的数据进行从小到大的排序(欧式距离中数值越小,越相似),获取一个由索引位置组成的数组
- 对这个索引位置取前k个,然后对前k个数据以标签(目标变量)作为key,然后value是count的累加
- 再对这个计数的map进行排序,根据value进行从大到小的排序
- 最后获取这个排名第一的数据,就是最相似的数据
4.2 欧式距离
下面的公式还是比较简单的,我们这里简单说下变量的含义
比如我们有一个数据集是5个特征的,那么
- i:就是每次的轮询数字,因为这里的n是5,所以i依次为1,2,3,4,5
- n:就是最大的数字,5
- Σ:这个符号的含义是求和对后面的公式所计算出的值求和,i~n就是每次要带入公式的i的值
- xi:我们知道i会分别为1,2,3,4,5,所以x1代表第一个特征,x2代表第二个特征,..
- yi:与xi同理
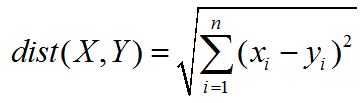
5 代码
import operator
from numpy import *
class kNN(object):
def createDataSet(self):
"""
创建测试数据集
:return:矩阵,标签
"""
group = numpy.array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
labels = ['A', 'A', 'B', 'B']
return group, labels
def classify0(self, inX, dataSet, labels, k):
"""
k-近邻,欧式距离计算两个向量的距离
:param inX: 输入向量
:param dataSet: 训练样本集
:param labels: 标签向量
:param k: 最近邻居的数目
:return: 最近的结果
"""
# 计算欧式距离
# 获得行数
dataSetSize = dataSet.shape[0]
# 将向量inx纵向复制变成矩阵跟dataSet的数量一样,再减去数据集
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
# 矩阵平方
sqDiffMat = diffMat ** 2
# 矩阵每行求和
sqDIstances = sqDiffMat.sum(axis=1)
# 数组每个值开方
distances = sqDIstances ** 0.5
# 数组值从小到大的索引号
sortedDistIndicies = distances.argsort()
# 选最距离最小的k个距离
classCount = {}
for i in range(k):
# 通过索引值获取标签
voteIlabel = labels[sortedDistIndicies[i]]
# 累加次数
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
# 根据次数从大到小排序
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
if __name__ == '__main__':
kNN = kNN()
group, labesl = kNN.createDataSet()
result = kNN.classify0([0, 0], group, labesl, 3)
print(result)
上面的代码的结果是B!
这么简单的代码,你应该看懂了吧
6 实战
经过上面的简单计算后,也进入我们的实战项目了!下面我们将计算一个手写识别系统的简单小项目吧!
6.1 数据准备
首先,我们的数据可以通过我的github进行下载!点我
digits目录存放的就是我们所要需要的数据!
6.2 算法准备
首先我们在写程序的时候,要经历哪些步骤呢?
- 查看数据,数据是怎么样子的?如何将数据离散为特征
- 写特征转化算法,将单条数据转化为向量,多条数据转化为矩阵
- 输入测试向量,测试算法模型的准确率!
import numpy
import operator
from numpy import *
class kNN(object):
def img2vector(self, filename):
"""
图片txt转向量
:param filename: 文件名
:return: 向量
"""
# 创建一个1024维度的向量
return_vec = numpy.zeros((1, 1024))
# 将数据导入到向量
with open(filename) as fr:
for i in range(32):
line = fr.readline()
# 导入一行数据(32个数字)
for j in range(32):
# 每个数字依次导入
return_vec[0, i * 32 + j] = int(line[j])
return return_vec
def classify0(self, inX, dataSet, labels, k):
"""
k-近邻,欧式距离计算两个向量的距离
:param inX: 输入向量
:param dataSet: 训练样本集
:param labels: 标签向量
:param k: 最近邻居的数目
:return: 最近的结果
"""
# 计算欧式距离
# 获得行数
dataSetSize = dataSet.shape[0]
# 将向量inx纵向复制变成矩阵跟dataSet的数量一样,再减去数据集
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
# 矩阵平方
sqDiffMat = diffMat ** 2
# 矩阵每行求和
sqDIstances = sqDiffMat.sum(axis=1)
# 数组每个值开方
distances = sqDIstances ** 0.5
# 数组值从小到大的索引号
sortedDistIndicies = distances.argsort()
# 选最距离最小的k个距离
classCount = {}
for i in range(k):
# 通过索引值获取标签
voteIlabel = labels[sortedDistIndicies[i]]
# 累加次数
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
# 根据次数从大到小排序
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
def handle_write_class_test(self, train_data_dirname, test_data_dirname):
# 加载训练集
labels = []
train_file_list = os.listdir(train_data_dirname)
train_data_count = len(train_file_list)
matrix = numpy.zeros((train_data_count, 1024))
for i in range(train_data_count):
file_name_ext = train_file_list[i]
file_name = file_name_ext.split(".")[0]
file_num = int(file_name.split("_")[0])
labels.append(file_num)
matrix[i, :] = self.img2vector("%s/%s" % (train_data_dirname, file_name_ext))
# 加载测试集
test_file_list = os.listdir(test_data_dirname)
err_count = 0.0
test_data_count = len(test_file_list)
for i in range(test_data_count):
file_name_ext = test_file_list[i]
file_name = file_name_ext.split(".")[0]
file_num = int(file_name.split("_")[0])
test_vec = self.img2vector("%s/%s" % (test_data_dirname, file_name_ext))
# 测试
result = self.classify0(test_vec, matrix, labels, 3)
bool_result = result == file_num
if not bool_result:
err_count = err_count + 1.0
print("result:%s, real:%d, bool:%s" % (result, file_num, bool_result))
print("error count:%f" % (err_count / float(test_data_count)))
if __name__ == '__main__':
train_dir = "../data/digits/trainingDigits"
test_dir = "../data/digits/testDigits"
kNN = kNN_2_3_2()
kNN.handle_write_class_test(train_dir, test_dir)
最后我们得到下面的结果,错误率约等于1.2%,这个效果还不错!
...
result:0, real:0, bool:True
result:0, real:0, bool:True
result:4, real:4, bool:True
result:9, real:9, bool:True
result:7, real:7, bool:True
result:7, real:7, bool:True
result:1, real:1, bool:True
result:5, real:5, bool:True
result:4, real:4, bool:True
result:3, real:3, bool:True
result:3, real:3, bool:True
error count:0.011628
