1 概述
决策树本质上是数据结构中的树,不过有一些区别是,树的根节点和中间节点都是判断,而树的边都条件,而所有叶子节点都是一些结果。其实本质上就是if-else,不过这个if-else是通过算法来构建出的树状if-else
一些决策树采用二分法划分数据,我们在这里主要使用ID3算法进行划分数据集,后续还会介绍C4.5和CART的决策树算法
2 优缺点
- 优点:计算复杂度不高,输出结果容易理解,对中间值的缺失不敏感,可以处理不相关特征数据,可以保存成模型
- 缺点:可能参数过渡匹配问题
- 适用数据范围:数值型和标称型
3 数据准备
3.1 数据准备
- 要测试的向量。是我们要进行预测的数据
- 训练数据集,包含目标向量的特征数据集
- 各个特征的标签名词
3.2 信息增益
划分数据集的最大原则是将无序的数据变得更加有序。那么使用信息论来度量信息就是一种组织杂乱无章数据的一种方法。
在划分数据集之前之后,信息发生的变化,我们称为信息增益,划分数据集时,获取信息增益最高的特征就是最好的选择。那么如何计算信息增益呢?这里我们可以通过熵来计算数据的信息增益。
除了这个方法外,还有个叫基尼不纯度的方法去度量集合的无序程度,就是从一个数据集中随机选取子项,度量其被错误分类到其他分组的概率,这里就不详细说这个方法啦。
3.3 熵
熵:一般意义上指的都是信息熵。就是信息的期望度,换个说法,就是信息的不确定性,因为不确定,所以期望。期望度越大,熵越高(不确定性越大,熵越高),反之,熵越高,混合的数据越多。(除了信息熵,还有相对熵)
下面是熵的计算公式
- Σ:求和,不赘述了
- n:特征的数量
- p(xi):这个特征值出现概率
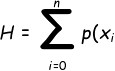
下面的代码就是用来求熵的:
import math
class trees(object):
def cal_shannonnt_entropy(self, data_set):
"""
通过最后一列计算香农熵(熵:信息的期望度)
公式:
X 标签出现的概率
n 标签分类的数量
---
H = - \ n
/ i=1 P(Xi)*log P(Xi)
--- 2
:param data_set: 数据集
:return: 香农熵
"""
# 数据行数
data_set_len = len(data_set)
# 数据中的 标签——数量
labels_count = {}
# 遍历数据
for vec in data_set:
# 获取标签
current_label = vec[-1]
# 初始化标签
if current_label not in labels_count.keys():
labels_count[current_label] = 0
# 标签计数
labels_count[current_label] += 1
# 香农熵
shannon_entropy = 0.0
for key in labels_count:
# 计算标签出现的概率P(Xi)
prob = float(labels_count[key]) / data_set_len
# 计算累减P(Xi)*log2P(Xi)
shannon_entropy -= prob * math.log(prob, 2)
return shannon_entropy
3.4 划分数据集
分类算法除了要测量信息熵,还要划分数据集,度量划分数据集的熵来判断当前是否争取的划分数据集。我们将每个特征划分数据集的结果计算一次熵,然后判断按照哪个特征划分数据集是最好的。
其实就是计算信息增益,算法就是矩阵的基础熵-划分该特征后的熵,这样对每个特征的信息增益求出后,取最大的那个,就是信息增益最好的那个
下面的代码,就是如何划分数据集和如何选择信息增益最好的那个!
class trees(trees_3_1_1):
def split_dataset(self, dataset, axis, value):
"""
筛选并重新划分数据集
axis位置等于value 并且 将这列去除
:param dataset: 数据集
:param axis: 位置
:param value: 值
:return:
"""
ret_dataset = []
for vec in dataset:
# 如果某个位置等于某值
if vec[axis] == value:
# 将这列抽出不要,生成新的向量
temp_vec = vec[:axis]
temp_vec.extend(vec[axis + 1:])
# 向量追加到矩阵
ret_dataset.append(temp_vec)
return ret_dataset
def choose_best_feature_to_split(self, dataset):
"""
计算最佳的数据集划分方式(本质上就是找到熵最小的那个特征字段)
通过比较各特征的信息增益来计算(信息增益:基础熵-划分该字段后的熵)
:param dataset:
:return:
"""
# 向量维度(矩阵列长)
feature_count = len(dataset[0]) - 1
# 计算基础香农熵
base_entropy = self.cal_shannonnt_entropy(dataset)
# 最佳信息增益
best_info_gain = 0.0
# 最佳特征位置
best_feature_index = -1
# 遍历每一列
for i in range(feature_count):
# 将所有数据的某列值提取成一个向量
feature_list = [example[i] for example in dataset]
# set去重
unique_vals = set(feature_list)
new_entropy = 0.0
# 遍历去重后的数据
# 计算每种划分方式的熵
for value in unique_vals:
# 筛选数据生成子数据集
sub_data_set = self.split_dataset(dataset, i, value)
# 计算子数据集的熵
prob = len(sub_data_set) / float(len(dataset))
new_entropy += prob * self.cal_shannonnt_entropy(sub_data_set)
# 计算信息增益
info_gain = base_entropy - new_entropy
# 判断最大信息增益
if info_gain > best_info_gain:
# 保存最大信息增益
best_info_gain = info_gain
# 保存最大信息增益特征的位置
best_feature_index = i
return best_feature_index
4 原理
4.1 算法思想
- 准备上方所说的数据
- 输入新数据后,首先对特征标签向量进行复制一份,这样对这个标签向量修改时,不会影响原有结构
- 对数据集的最后一列进行抽取,也就是要把我们的最后的分类抽出,如果只有一个分类的话,直接返回
- 计算当前数据集的最佳划分方式,并获取这个特征的特征标签,以这个标签作为根节点创建一棵数
- 在特征标签变量中删除这个最佳划分方式的特征的标签
- 将所有数据的这个最佳划分方式的特征这一列的值抽取出来,然后去重
- 再对这个去重后的集合进行遍历,以这些特征值进行筛选划分数据集,然后递归计算这些数据集,返回的树作为当前树的字树
- 直到遍历完为止
5 代码
class trees(object):
def create_dataset(self):
dataSet = [
[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']
]
labels = ['不浮出水面能生存', '有脚蹼']
return dataSet, labels
def majority_cnt(self, class_list):
"""
返回出现次数最多的标签
:param class_list:
:return:
"""
class_count = {}
for vote in class_list:
if vote not in class_count.keys():
class_count[vote] = 0
class_count[vote] += 1
sorted_class_count = sorted(class_count.items(), operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0]
def create_tree(self, dataset, labels):
"""
生成决策树
:param dataset: 数据集
:param labels: 便签
:return:
"""
# 创建一个新的list,不对原有labels操作
labels=list(labels)
# 生成分类列表
class_list = [example[-1] for example in dataset]
# 如果只有一个分类则返回
if class_list.count(class_list[0]) == len(class_list):
return class_list[0]
# 如果只有一列的话,返回出现次数最多的标签
if len(dataset[0]) == 1:
return self.majority_cnt(class_list)
# 计算最佳的划分方式的特征字段位置
best_feature_index = self.choose_best_feature_to_split(dataset)
# 获取该字段所以代表的标签
best_feature_label = labels[best_feature_index]
# 初始化树
tree = {best_feature_label: {}}
# 删除最佳划分方式字段的标签
del (labels[best_feature_index])
# 将最佳划分方式的一列抽出来
feat_val = [example[best_feature_index] for example in dataset]
# set去重
unique_val = set(feat_val)
for val in unique_val:
sub_labels = labels[:]
# 通过最佳特征字段筛选并重新划分数据集
sub_dataset = self.split_dataset(dataset, best_feature_index, val)
# 递归遍历
tree[best_feature_label][val] = self.create_tree(sub_dataset, sub_labels)
return tree
if __name__ == '__main__':
tree = trees()
dataset, labels = tree.create_dataset()
m_tree = tree.create_tree(dataset, labels)
print(m_tree)
上面的代码的结果是{'不浮出水面能生存': {0: 'no', 1: {'有脚蹼': {0: 'no', 1: 'yes'}}}}!
这就是我们通过算法构建出的决策树,通过杂乱的数据来清洗的构造出这个决策树,是不是很神奇呢?
6 实战
经过上面的简单计算后,也进入我们的实战项目了!下面我们将构建一个预测隐形眼镜类型的简单小项目吧!
6.1 数据准备
首先,我们的数据可以通过我的github进行下载!点我
digits目录存放的就是我们所要需要的数据!
6.2 算法准备
首先我们在写程序的时候,要经历哪些步骤呢?
- 查看数据,数据是怎么样子的?
- 写特征转化算法,将单条数据转化为向量,多条数据转化为矩阵
- 输入训练数据,构建决策树
- 查看决策树的结构
class trees(objecy):
# 将上面的算法copy过来就行
pass
if __name__ == '__main__':
# 隐形眼镜数据集
filename = "../data/lenses.txt"
trees = trees()
lenses = []
with open(filename, 'r') as fr:
lenses = [line.strip().split('\t') for line in fr.readlines()]
labels = ["年龄", "病因", "散光", "泪液率"]
tree = trees.create_tree(lenses, labels)
print(tree)
最后我们得到下面的决策树,貌似匹配选项可能太多,有点复杂! 其实这个问题就叫做过渡匹配。
我们其实可以通过裁剪决策树,去掉一些不必要的叶子节点,如果子节点只能增加少许信息,则可以删除该节点。
{
"泪液率": {
"减少": "不适合戴",
"正常": {
"散光": {
"yes": {
"病因": {
"近视": "硬的",
"远视": {
"年龄": {
"年轻": "硬的",
"老人": "不适合戴",
"中年": "不适合戴"
}
}
}
},
"no": {
"年龄": {
"年轻": "软的",
"老人": {
"病因": {
"近视": "不适合戴",
"远视": "软的"
}
},
"中年": "软的"
}
}
}
}
}
}
