本篇内容含有大量公式,如果展示不佳,请跳转至原文
过年期间,我抽时间把深度学习的神经网络的数学基础学习了一下,简单的看了看神经网络的基础,在这里我通过写这个系列的博文来沉淀我所学到的知识。
1 生物学上的神经元
1.1 神经元的概念
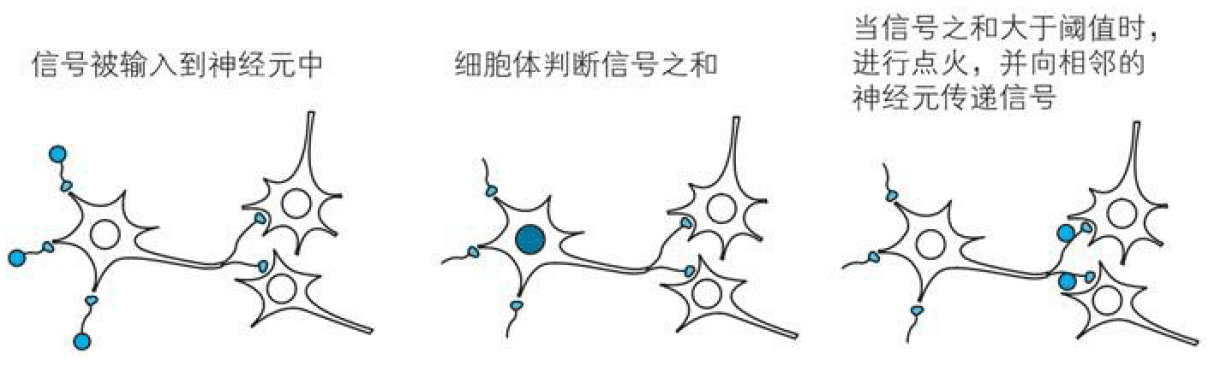
神经网络的这个想法,是受到生物学上的神经元的启发所创建出来的。在生物学上,神经元是以下方的流程来作出反应的。
- 神经元形成网络
- 从其他多个神经元传递过来的信号,如果他们的和不超过某个固定大小的值(阈值),则神经元不做出任何反应
- 如果他们的和超过某个固定大小的值(阈值),则神经元做出反应(称为
点火),向另外的神经元传递固定强度的信号 - 在2和3中,从多个神经元传递过来的信号中,每个信号对应的
权重是不同的。
1.2 神经元的工作
阈值:神经元固有的边界敏感值值
点火:神经元参数的和超过阈值,神经元对此作出反应
对于生命来说,神经元会忽略微笑的输入信号,这是十分重要的。
反之,如果神经元对于任何微小的信号都变得兴奋,那么这个神经系统将“情绪不稳定”
(想想网络上说的玻璃心是不是就是这个意思呢)
2 神经元的简单数学表示
上面我们说到神经元是通过将输入的信号的和是否超过阈值来判断是否点火,那么如果点火之后呢,点火的输出又是什么呢?
其实,神经元的点火输出也是信号,有意思的是,无论神经元接受到多大的刺激或很多很多神经元传来的信号,这个神经元也只输出固定大小的信号,比如点火后的输出是0或1。简单整理如下:
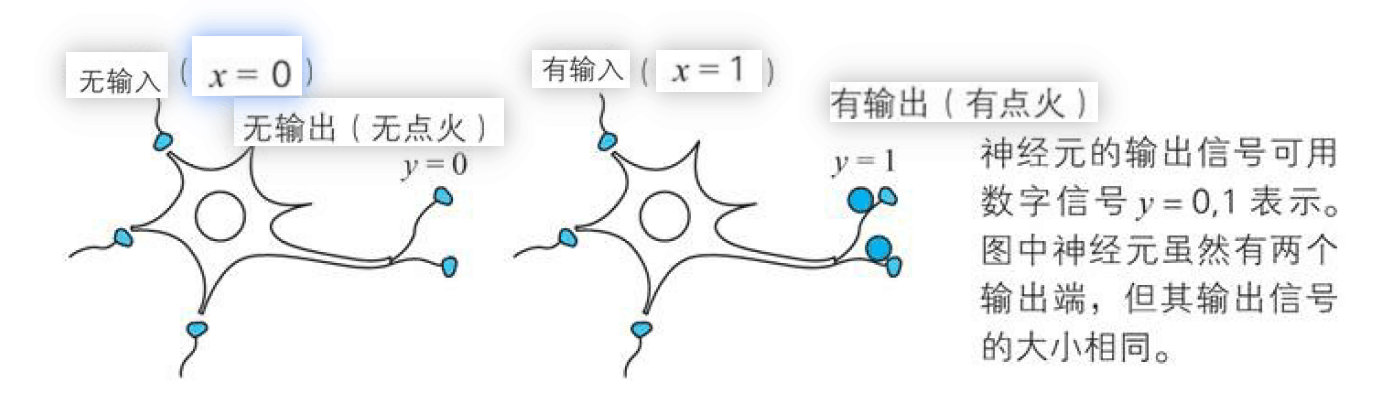
- 来自其他多个神经元的信号之和成为神经元的输入
- 如果输入超过神经元固有的阈值,则点火
- 神经元的点火输出可以用数字信号0和1来表示,及时有多个输出端,值也是同一个。
下面让我们用数学来简单的表示1-1中的流程吧:
2.1 输入
我们这里将神经元的阈值设置为0,大于阈值则点火,输入则分为$\le 0$和$>0$,也可以成为”有“、“无”两种输入信号。

2.2 输出
我们这里将神经元的点火设置为0和1两种信号。

则
2.3 权重
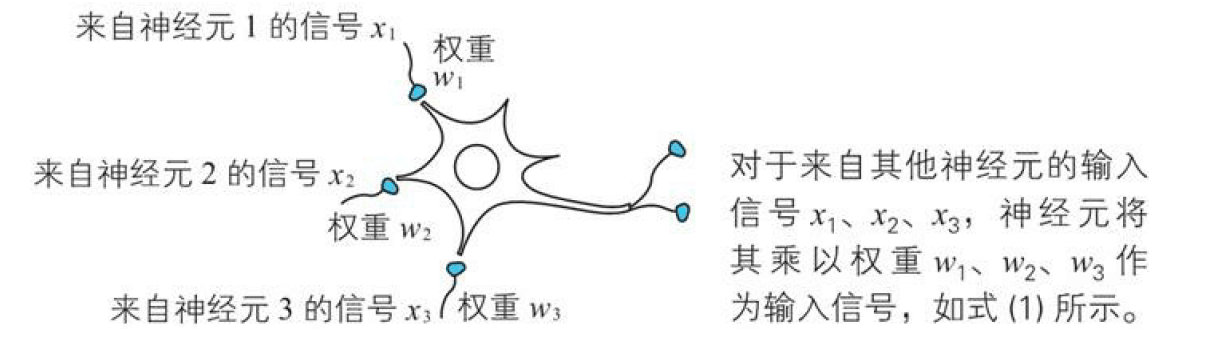
从上面我们知道。神经元点火与否是根据输入信号的和来判断的,但是这个求和的方式不是简单的求和,而是不同的输入的重要性不同,这个重要性系数就是我们的权重,比如打网球的时候,我们的视觉神经信号的是比听觉神经信号更重要的,那么视觉神经元和听觉神经元的权重就不同。
假设我们有三个神经元${x}_{1}$、${x}_{2}$、${x}_{3}$,则神经元的输入信号的和为: $${w}_{1}{x}_{1}+{w}_{2}{x}_{2}+{w}_{3}{x}_{3}$$
其中${w}_{1}$、${w}_{2}$、${w}_{3}$分别是输入信号${x}_{1}$、${x}_{2}$、${x}_{3}$对应的权重。
2.4 点火条件
根据上述,神经元在信号之和超过阈值时,点火,那么我们根据${w}_{1}{x}_{1}+{w}_{2}{x}_{2}+{w}_{3}{x}_{3}$推出,点火条件如下:
这里的 $\theta$ 代表
阈值
$$无输出信号(y=0):{w}_{1}{x}_{1}+{w}_{2}{x}_{2}+{w}_{3}{x}_{3}<\theta\\有输出信号(y=1):{w}_{1}{x}_{1}+{w}_{2}{x}_{2}+{w}_{3}{x}_{3}\ge \theta $$
例 1 来自两个神经元 1、2 的输入信号分别为变量$x_1$ 、$x_2$ ,权重为$w_1$ 、$w_2$,神经元的阈值为$\theta$ 。当$w_1=5$ ,$w_2=3$ ,$\theta=4$ 时,考察信号之和${w}_{1}{x}_{1}+{w}_{2}{x}_{2}$的值与表示点火与否的输出信号$y$的值。

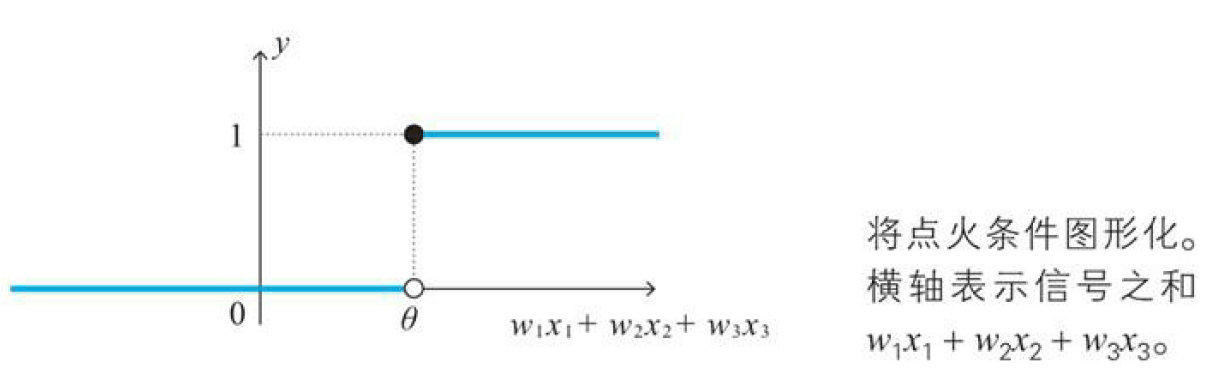
2.5 点火条件图形表示(阶跃函数)
下面我们将上方的点火条件函数进行图形化,以神经元的输入信号的和为横轴,神经元的输出信号y为纵轴,如下图所示:当信号之和小于$\theta$时,y取0,反之取1
如果用函数来表示这个图像,那么就需要用到下方的单位阶跃函数
$$u(z)=\left\{ \begin{matrix} 0\quad (z<0) \\ 1\quad (z\ge 0) \end{matrix} \right\} $$
阶跃函数图形如下:
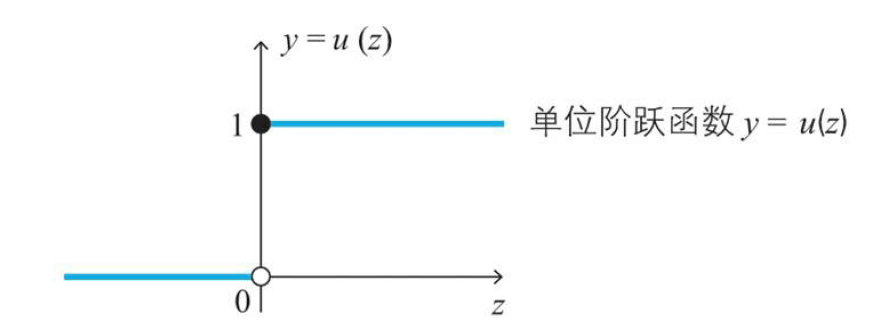
利用阶跃函数,我们将我们的神经元输入和阈值带入,可以推出我们的点火函数:
$$y=u(w_1x_1+w_2x_2+w_3x_3-\theta )$$
那么阶跃函数中的自变量z,我们就可以求出来了。这个z,我们又称作加权输入
$$z=w_1x_1+w_2x_2+w_3x_3-\theta $$
2.6 激活函数
下面的图是神经元的简化图
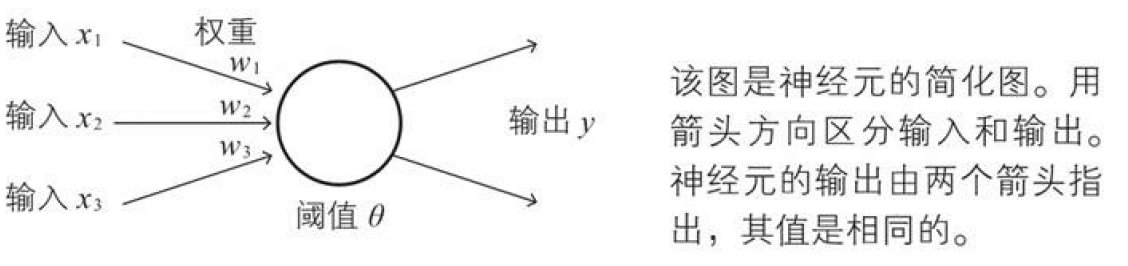
因为在上面说道在生物界,y的值为1或0,那么除去生物这个限制,我们就需要对我们的点火函数进行修改,这里我们把u变成a,这里的a通常是建模者定义的函数,成为激活函数。
$$y=a(w_1x_1+w_2x_2+w_3x_3-\theta )$$
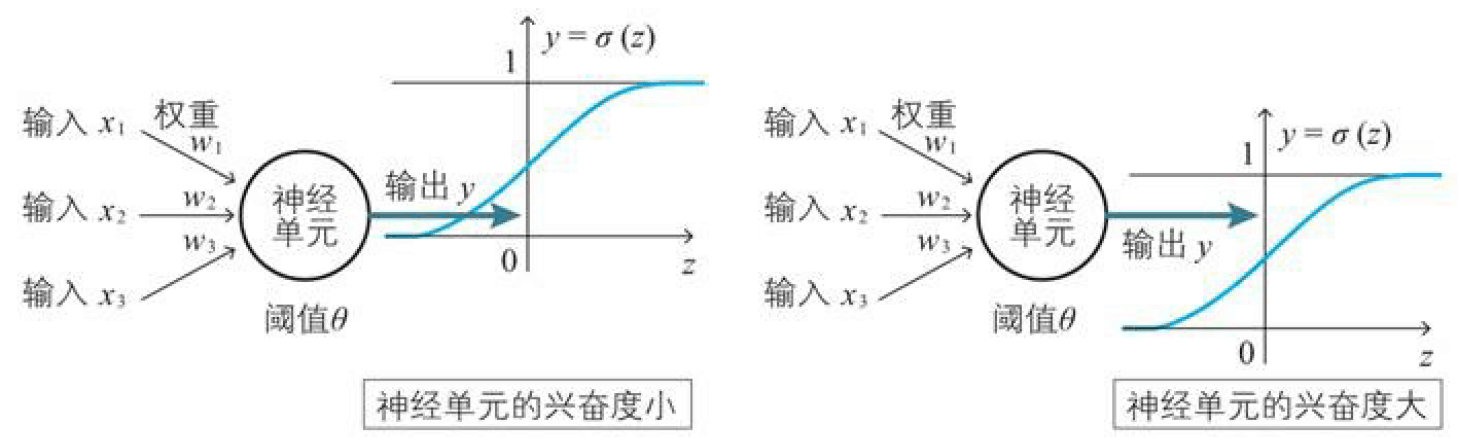
在上面这个函数中,y可以取到任何值。如果通俗一点的话,可以理解为这个y值是神经元的兴奋度、反应度、活性度
下面对比下两种神经元的差异:
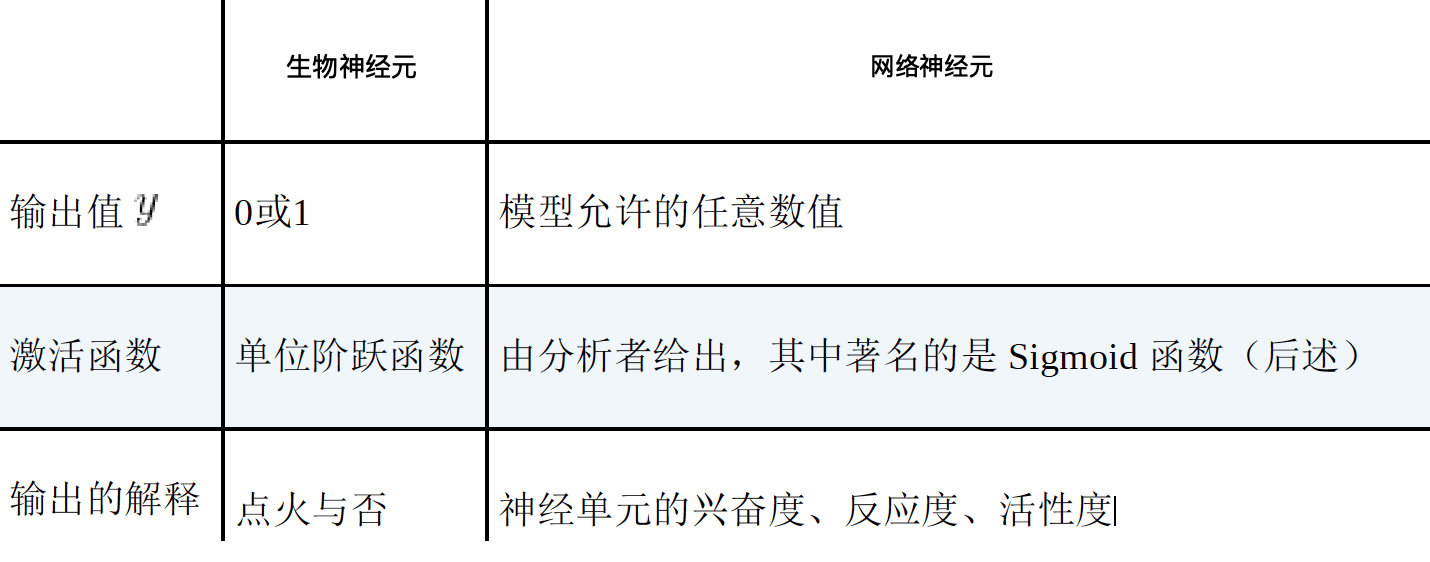
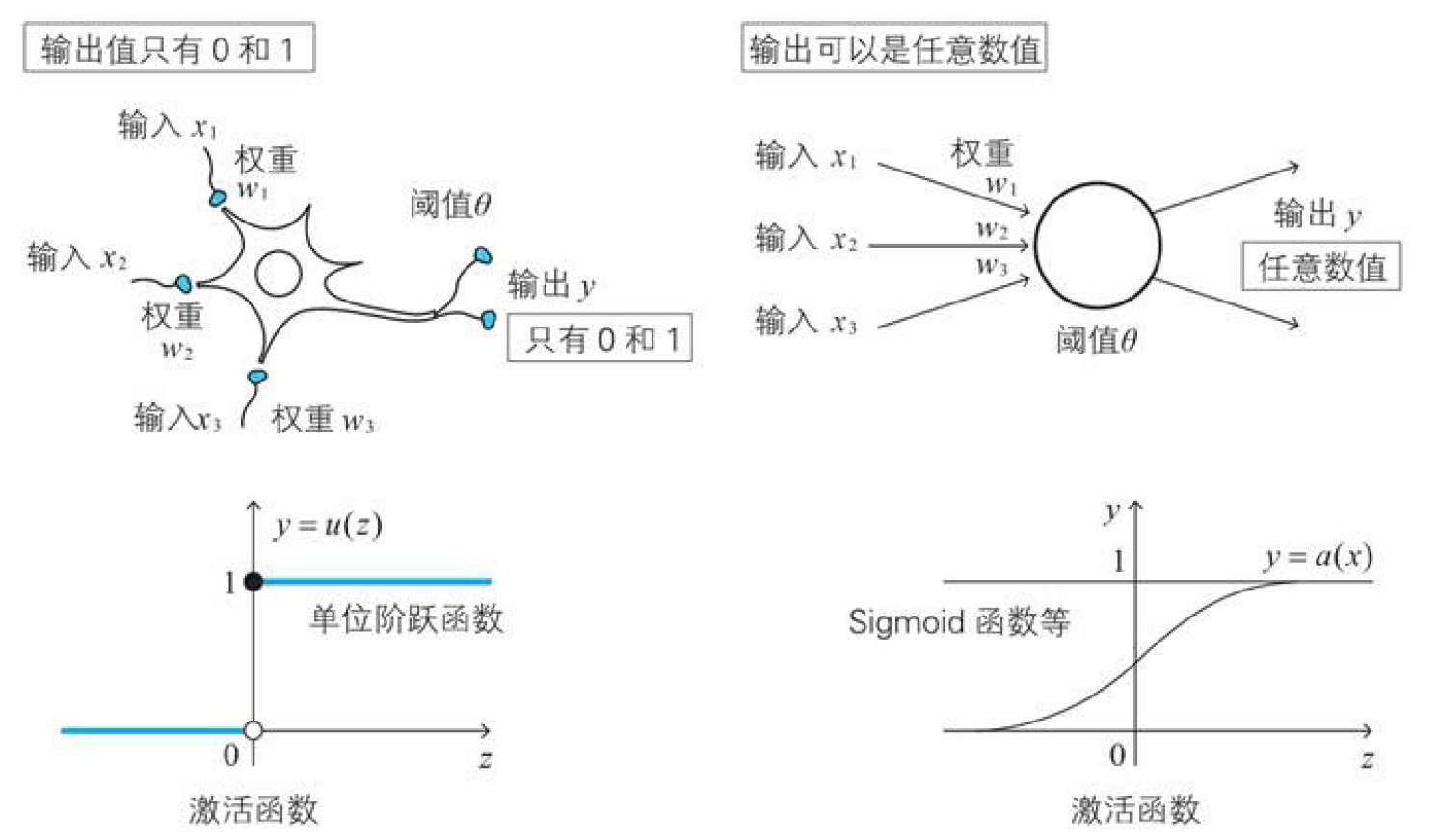
sigmoid函数
激活函数的代表性例子就是Sigmoid函数$\sigma (z)$,下面是它的定义:
$$\sigma (z)=\frac { 1 }{ 1+{ e }^{ -z }} (z\approx2.718281… )$$
这个函数的作用是将输入值转换到(0,1)区间,也就是说sigmoid函数的输出值是大于0且小于1的任意值。该函数最重要的特性是连续、光滑,也就代表着可导。有了这种性质就使得sigmoid函数会很容易处理
阶跃函数的输出值为0和1可代表点火与否,而sigmoid函数的输出值却在(0,1)区间,那么我们就要换个思路了,不能用其输出值代表点火与否,但是可用它的输出值代表神经元的兴奋度,越接近1越兴奋。
我们将主要使用sigmoid来作为标准的激活函数使用,如果使用数学上单调递增的可导函数来代替sigmoid作为激活函数,那么也是可以的.
2.7 偏置
我们再来看下我们的激活函数: $$y=a(w_1x_1+w_2x_2+w_3x_3-\theta )$$
这里的$\theta$我们称为阈值,在生物学上是神经元特性的值,通俗的讲$\theta$表示为神经元的感受能力,如果$\theta$较大,我们的神经元会不容易兴奋(就是迟钝),如果$\theta$较小,则神经元会很容易兴奋(特别敏感)
上面的式子中$\theta$有负号,这帮搞数学的觉着负号不好看,认为减法容易算错,非要把负号干掉,所以就把$-\theta$替换为了$b$,于是就有了下面这两个式子:
下面这两个式子是神经网络的出发点,非常重要
$$z=w_1x_1+w_2x_2+w_3x_3+b $$ $$y=a(z)=a(w_1x_1+w_2x_2+w_3x_3+b )$$
变成了这个样子,式子好看了,也不容易错了,于是这个$b$就叫做偏置
生物学上的$w_1$、$w_2$、$w_3$和阈值$\theta$($-b$)都不是负数,因为负数不会在自然现象中出现,但是我们将神经元一般化后,是允许出现负数的。
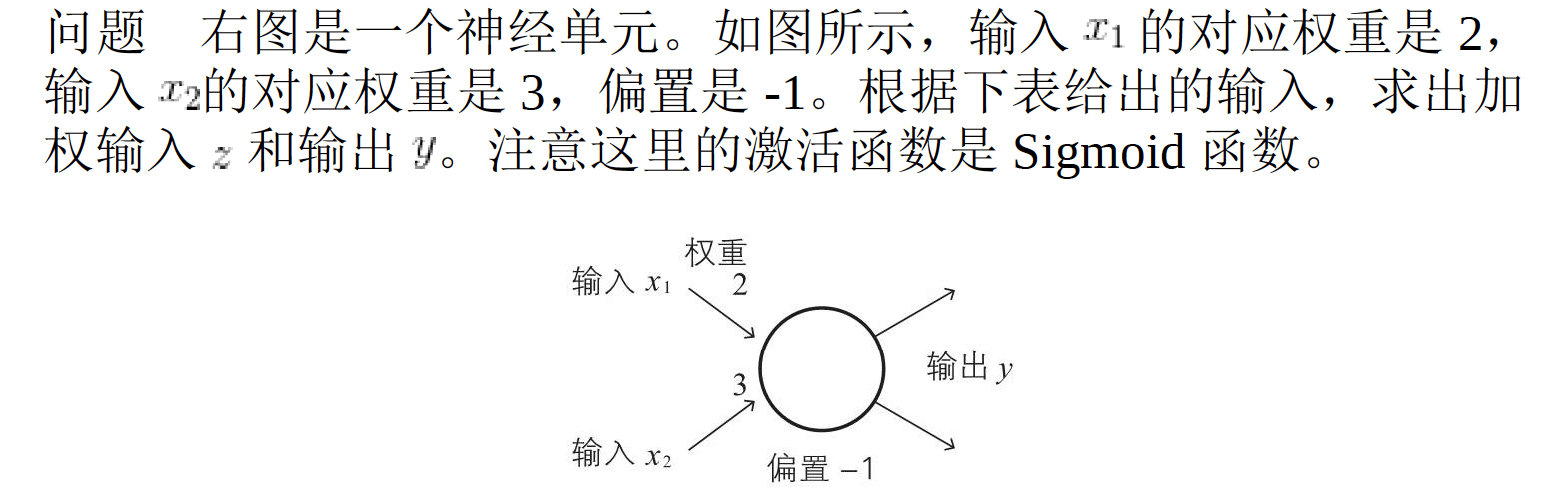

上面我们用一个例子来验证我们所学到的知识。相信很多人的算法就像上方表格中的加权输入z一样,其实对于计算机来说有一种更加容易的计算方式,那就是线性代数中的内积。
我们将变量$x_1$、$x_2$、$x_3$作为变量向量,将权重$w_1$、$w_2$、$w_3$和偏执$b$作为一个参数向量,通过计算两个向量的内积来计算z,这时我们发现变量向量的长度是3,而权重和偏执的向量是4,所以我们需要使用1作为b的系数加入到变量向量中。
$$\left[ x_1 ,x_2,x_3,1\right]\\\\\left[ w_1 ,w_2,w_3,b\right]\\=w_1x_1+w_2x_2+w_3x_3+1*b$$
这不就是我们上方使用的算法吗,这种向量的内积的计算方式虽然对人不太友好,但是计算机却更加擅长这种计算,在我们真正撸代码的时候会用到这种方法。
