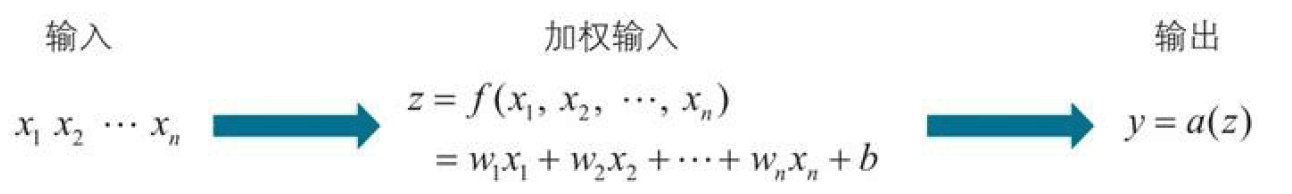$$\begin{cases} z=f(x_{ 1 },x_{ 2 },…,x_{ n })\\=w_{ 1 }x_{ 1 }+w_{ 2 }x_{ 2 }+…+w_{ n }x_{ n }+b \\ y=a(z) \end{cases}$$
本篇内容含有大量公式,如果展示不佳,请跳转至原文
上次讲了导数和偏导数的基础,那么这些还不足以使用起来,今天就来讲讲误差反向传播中用来解决复杂函数求导的链式法则。
1 复合函数
已知函数$y=f(u)$,当$u$表示为$u=g(x)$时,y作为x的函数就可以表示为$y=f(g(x))$这样的嵌套结构,这种嵌套结构的函数,就称为$f(u)$、$g(x)$的复合函数
示例1:函数$z={(2-y)}^{2}$是函数$u=2-y$和函数$z=u^2$的复合函数。
示例2:对于多个输入$x_1,x_2,…,x_n$,将$a(x)$作为激活函数,求神经单元的输出$y$的过程 $$y=a(w_1x_1+w_2x_2+…+w_nx_n+b)$$ $w_1,w_2,…,w_n$为各输入对应的权重,$b$为神经单元的偏置,这个输出函数是如下的$x_1,x_2,…,x_n$的一次函数$f$和激活函数$a$的复合函数 $$\begin{cases} z=f(x_{ 1 },x_{ 2 },…,x_{ n })\\=w_{ 1 }x_{ 1 }+w_{ 2 }x_{ 2 }+…+w_{ n }x_{ n }+b \\ y=a(z) \end{cases}$$
2 链式法则
2.1 单变量函数链式法则
已知单变量函数$y=f(u)$,当$u$表示为单变量函数$u=g(x)$时,复合函数$f(g(x))$的导函数可以如下简单地求出来。 $$\frac { dy }{ dx } =\frac { dy }{ du } \frac { du }{ dx } $$
上面这个公式称为单变量函数的复合函数求导公式,也称为链式法则。
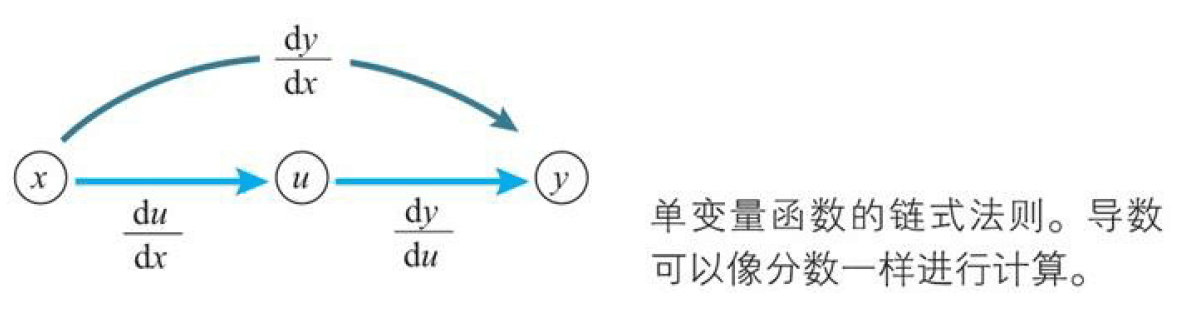
公式的右边,如果将$dx$、$dy$、$du$都看作一个单独的字母,那么公式的左边可以看作将右边进行简单的约分的结果,这个看法总是成立的。通过将导数用$dx$、$dy$等表示,我们可以这样记忆链式法则:复合函数的导数可以像分数一样使用约分。,但是这个约分的法则不适用于$dx$、$dy$的平方等情形。
示例:当$y$为$u$的函数,$u$为$v$的函数,$v$为$x$的函数时 $$\frac { dy }{ dx } =\frac { dy }{ du } \frac { du }{ dv } \frac { dv }{ dx } $$
下面我们来试试对sigmoid与wx+b的复合函数进行求导吧
示例:对$x$的函数 $y=\frac { 1 }{ 1+{ e }^{ -(wx+b) } }$($w$、$b$为常数)求导 我们设以下函数 $$y=\frac { 1 }{ 1+{ e }^{ -x } },u=wx+b $$ 由于第一个式子为Sigmoid函数,根据在上篇文章中讲的sigmoid函数的导数如下所示 $$\frac { \partial y }{ \partial u } =y(1-y)$$ 第二个式子$wx+b$,它的导数则是 $$\frac { \partial u }{ \partial x } =w$$ 那么上面的式子的导数则是 $$\frac { \partial y }{ \partial x } =\frac { \partial y }{ \partial u } \frac { \partial u }{ \partial x } =y(1-y)w=\frac { 1 }{ 1+{ e }^{ -(wx+b) } } \left( 1-\frac { 1 }{ 1+{ e }^{ -(wx+b) } } \right) $$
2.2 多变量函数链式法则
在多变量函数的情况下,链式法则的思想也同样适用。只要像处理分数一样对导数的式子进行变形就行了,但是事情并没有想的那么简单,因为必须要对相关的全部变量应用链式法则。
让我们来看看两个变量的情形。变量$z$为$u$、$v$的函数,如果$u$、$v$分别为$x$、$y$的函数,则$z$为$x$、$y$的函数,此时下方的多变量函数的链式法则成立。
$$\frac { \partial z }{ \partial x } =\frac { \partial z }{ \partial u } \frac { \partial u }{ \partial x } +\frac { \partial z }{ \partial v } \frac { \partial v }{ \partial x } $$

变量$z$为$u$、$v$的函数,$u$、$v$分别为$x$、$y$的函数,$z$关于$x$求导时,先对$u$、$v$求导,然后与$z$的相应导数相乘,最后将乘积加起来。
z关于y求导时,也是如此。下方式子依旧成立。
$$\frac { \partial z }{ \partial y } =\frac { \partial z }{ \partial u } \frac { \partial u }{ \partial y } +\frac { \partial z }{ \partial v } \frac { \partial v }{ \partial y } $$

示例1:当 $C=u^2+v^2$,$u=ax+by$,$v=px+qy$ (a、b、p、q为常数)时,关于$x$、$y$的导数如下所示。 $$\frac { \partial C }{ \partial x } =\frac { \partial C }{ \partial u } \frac { \partial u }{ \partial x } +\frac { \partial C }{ \partial v } \frac { \partial v }{ \partial x } =2u\cdot a+2v\cdot p=2a(ax+by)+2p(px+qy)$$ $$\frac { \partial C }{ \partial y } =\frac { \partial C }{ \partial u } \frac { \partial u }{ \partial y } +\frac { \partial C }{ \partial v } \frac { \partial v }{ \partial y } =2u\cdot b+2v\cdot q=2b(ax+by)+2p(px+qy)$$ 上式在三个以上的变量的情况下也同样成立
示例2:当 $C=u^2+v^2+w^2$,$u=a_1x+b_1y+c_1z$,$v=a_2x+b_2y+c_2z$,$w=a_3x+b_3y+c_3z$($a_i$、$b_i$、$c_i$为常数,i=1,2,3)时,求关于x的偏导数 $$\frac { \partial C }{ \partial x } =\frac { \partial C }{ \partial u } \frac { \partial u }{ \partial x } +\frac { \partial C }{ \partial v } \frac { \partial v }{ \partial x } +\frac { \partial C }{ \partial w } \frac { \partial w }{ \partial x } \\ =2u\cdot { a }_{ 1 }+2v\cdot { a }_{ 2 }+2w\cdot { a }_{ 3 }\\ =2{ a }_{ 1 }({ a }_{ 1 }x+b_{ 1 }y+{ c }_{ 1 }z)+2{ a }_{ 2 }({ a }_{ 2 }x+b_{ 2 }y+{ c }_{ 2 }z)+2{ a }_{ 3 }({ a }_{ 3 }x+b_{ 3 }y+{ c }_{ 3 }z)$$