目录 x

本篇内容含有大量公式，如果展示不佳，请跳转至原文

1 向量基础

向量就是具有大小和方向的量。

1.1 有向线段与向量

有两个点$A、B$，我们考虑从$A$指向$B$的线段，这条具有方向的线段$AB$叫作有向线段。我们称$A$为起点，$B$为终点。

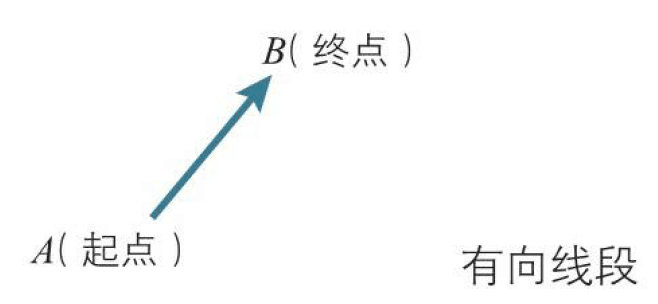
有向线段$AB$具有以下属性：

起点$A$的位置
指向$B$的方向，
$AB$的长度，也就是大小。

在这3个属性中，把方向与大小抽象出来，这样的量叫作向量，通常用箭头表示。

向量是具有方向与大小的量，用箭头表示。

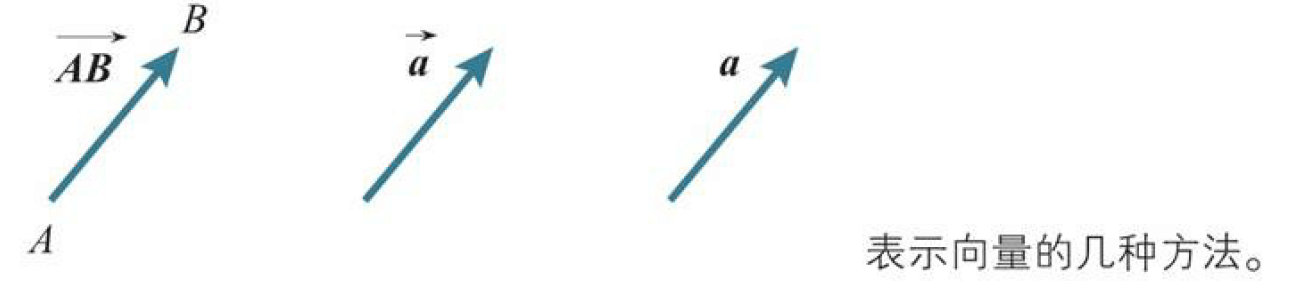
有向线段$AB$所代表的向量用$\overrightarrow{AB}$表示，也可以用带箭头的单个字母$\vec{a}$或者不带箭头的黑斜体字母a表示。

1.2 向量的坐标表示

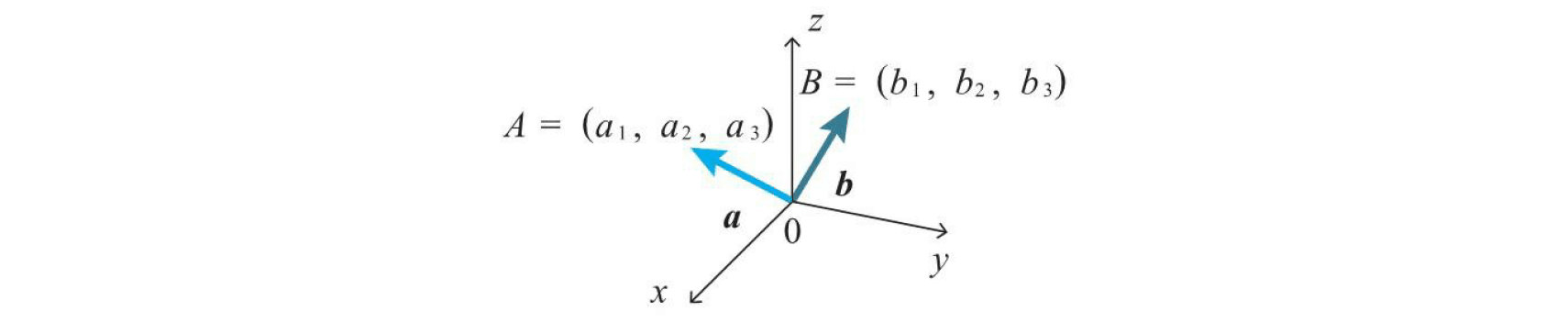
把箭头的起点放在原点，用箭头终点的坐标表示向量，这叫作向量的坐标表示。用坐标表示的向量$a$如下所示（平面的情况）。 $$a=(a_1,a_2)$$

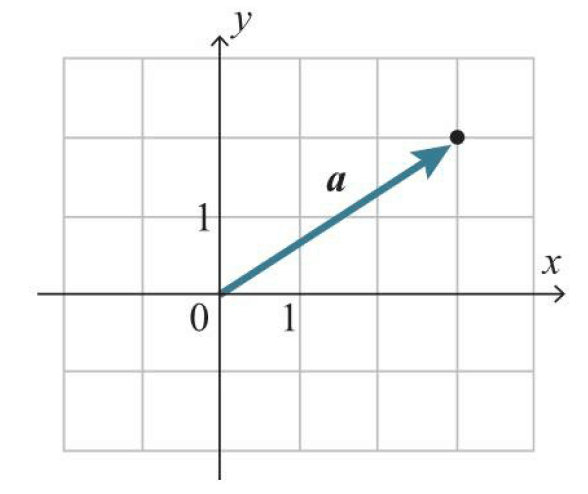
示例：$a=(3,2)$表示的向量。

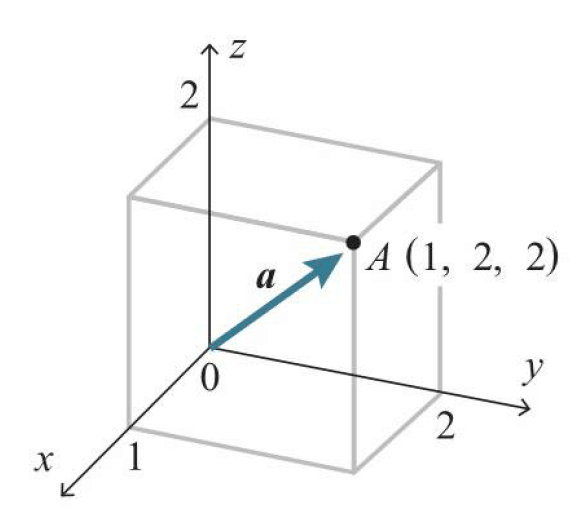
示例：在三维空间的情况下也是同样的。例如， $a=(1,2,2)$表示下图所示的向量。

1.3 向量的大小

通俗的讲，表示向量的箭头的长度称为这个向量的大小。向量$a$的大小用$\left|a\right|$(绝对值)表示。

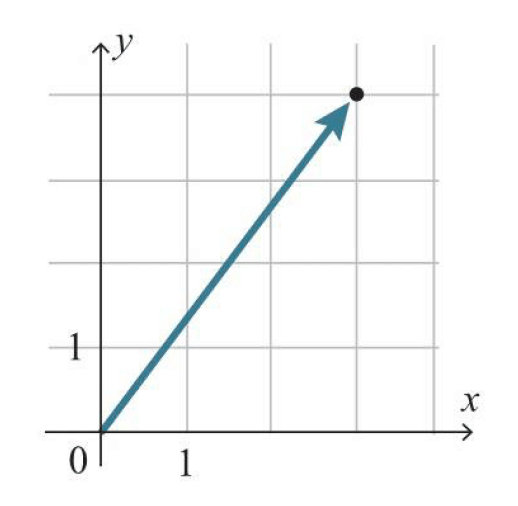
示例：根据下图，如下求得$a=(3,4)$的大小$\left|a\right|$。 $$\left| a \right| =\sqrt { 3^2+4^2 }=5 $$

看到这里，是不是感觉很熟悉，欧股定理！上面是二维的，下面看看三维的把！

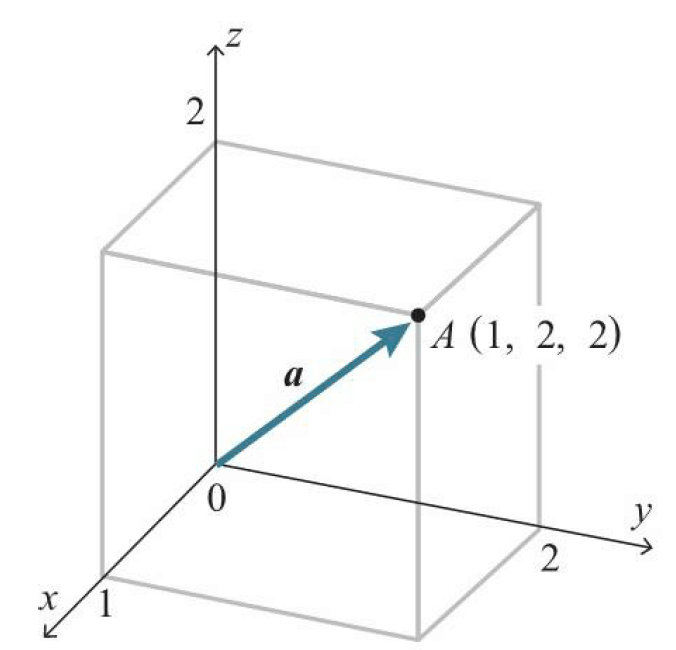
示例：求得下图所示的向量$a=(1,2,2)$的大小$\left|a\right|$。 $$\left| a \right| =\sqrt { 1^2+2^2+2^2 }=3 $$

看到这里，我们就应该明白了，多维跟二维是一样的，都是使用勾股定理。 $$\left| a \right| =\sqrt { { (x_1) }^{ 2 }+{ (x_2) }^{ 2 }+{ (x_{…}) }^{ 2 }} $$

1.4 向量的内积

我们在考虑具有方向的向量的乘积时，包含了“方向与方向的乘积”这样不明确的概念。因此，我们需要一个新的定义叫内积。

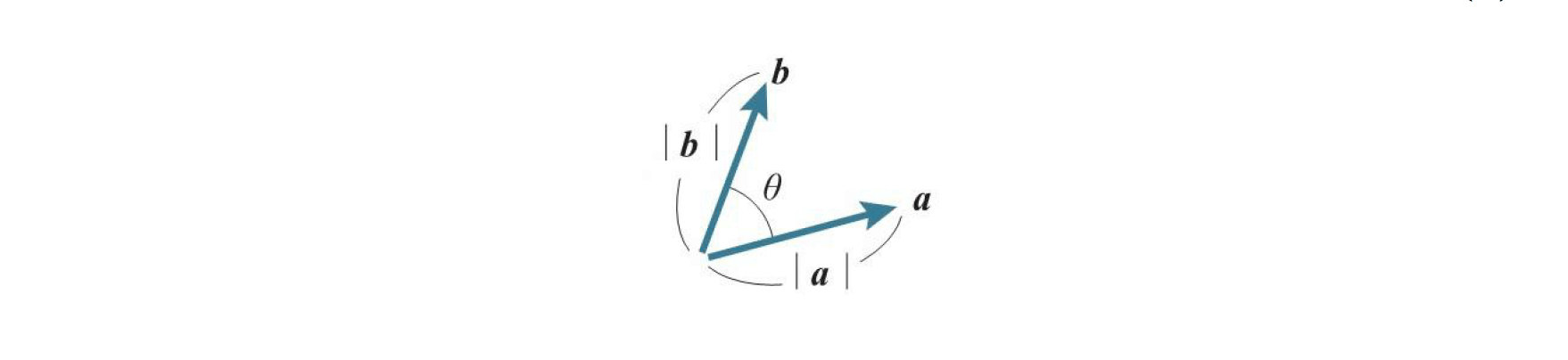
两个向量$a$、$b$的内积$a\cdot b$的公式如下 $$a\cdot b=\left| a \right| \left| b \right| \cos { \theta } $$

示例：考虑边长为1的正方形$ABCD$，$\overrightarrow { AB }=a $，$\overrightarrow{AD}=b$，$\overrightarrow{AC}=c$，求$a$向量与另外两个向量之间的内积 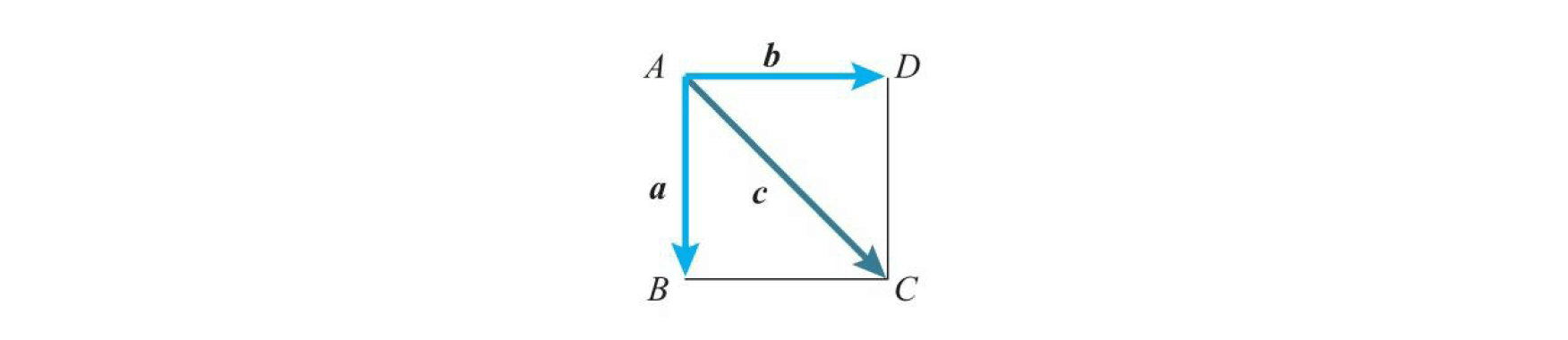$$\left|a\right|=\left|b\right|=1,\left|c\right|=\sqrt {2} $$ $a$与$b$的夹角为$90°$，$a$与$c$的夹角为$45°$,所以 $$a\cdot b=\left| a \right| \cdot \left| b \right| \cdot \cos { 90° } =1\times 1\times 0=0\\ a\cdot c=\left| a \right| \cdot \left| c \right| \cdot \cos { 45° } =1\times \sqrt { 2 } \times \frac { 1 }{ \sqrt { 2 } } =1$$

三维或更高维度的向量内机同样使用上方的公式

1.5 柯西·施瓦茨不等式

证明： $$\because -1\le \cos { \theta } \le 1\\ \therefore 两边同时乘以\left| a \right|\left| b \right|得\left| a \right| \left| b \right| \le \left| a \right| \left| b \right| \cos { \theta } \le \left| a \right| \left| b \right| \\ \because 上面的内积公式a\cdot b=\left| a \right| \left| b \right| \cos { \theta } \\ \therefore 带入后得-\left| a \right| \left| b \right| \le a \cdot b\le \left| a \right| \left| b \right| $$

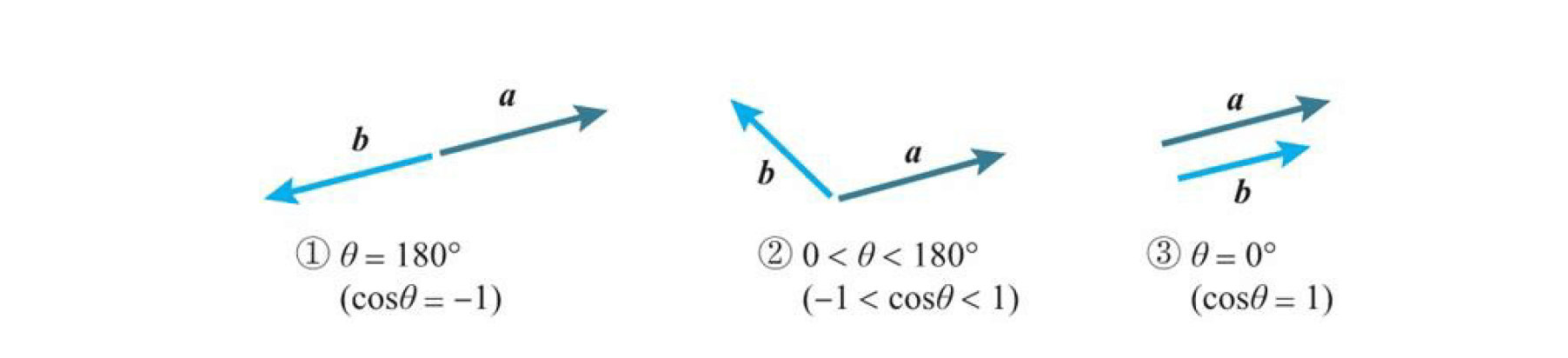分析发现，共有以上三种情况，在这三种情况下，我们推导出下面三种性质，后面会说到的梯度下降就是使用下面第一个性质

当两个向量方向相反时，内积取得最小值。即$\cos { \theta } =-1时，\cos { \theta } \left| a \right| \left| b \right| =-\left| a \right| \left| b \right| $
当两个向量不平行时，内积取平行时的中间值。即$-1<\cos { \theta } <1时，\cos { \theta } \left| a \right| \left| b \right| =\cos { \theta } \left| a \right| \left| b \right| $
当两个向量方向相同时，内积取得最大值。即$\cos { \theta } =1时，\cos { \theta } \left| a \right| \left| b \right| =\left| a \right| \left| b \right| $

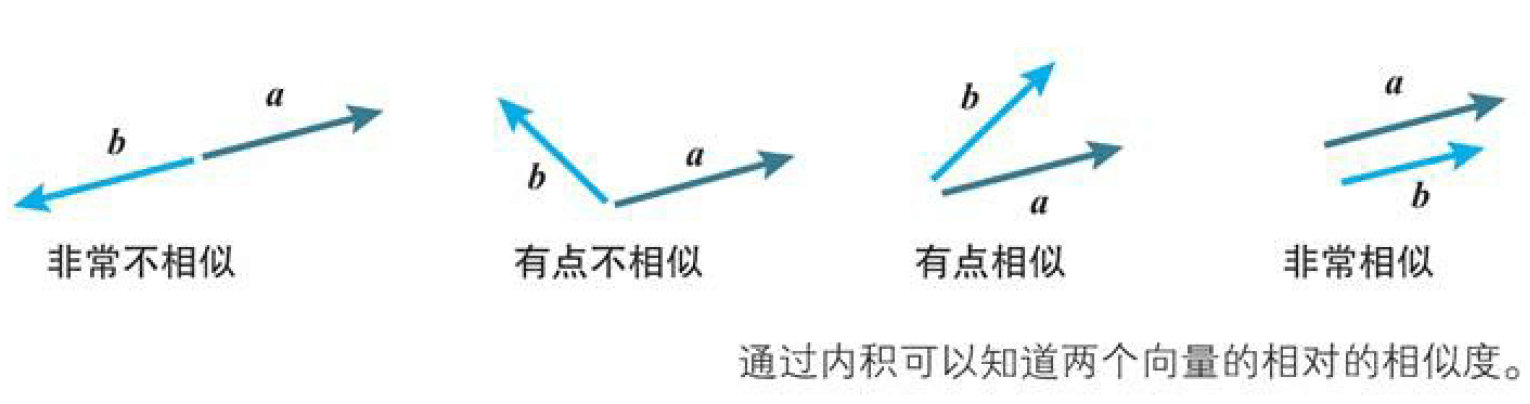
同时，通过上方的公式，我们也可以发现内积的另一个意义就是两个向量在方向上的相似度，内积越大，两个向量的方向越相似，比如余弦相似度算法就是基于内积的

1.6 内积的坐标表示

上面，我们讲到了如何求两个向量的内积，那么如何用坐标来表示两个向量的内积呢？其实很简单，就对应位置的值相乘，公式如下 $$当a=(a_1,a_2,a_{…}),b=(b_1,b_2,b_{…})时$$ $$a \cdot b=a_1b_1+a_2b_2+a_{…}b_{…}$$

示例：当$a=(2,3),b=(5,1)$时，$a\cdot b$为多少？ $$a\cdot b=2\times 5+3\times 1=13$$

多维空间也是如此。 $$a \cdot b=a_1b_1+a_2b_2+a_3b_3$$

还记得我们在之前的文章深度学习数学基础(一)之神经元构造中最后说到的神经元的输出使用内积的计算方式吗？其实就是使用了这里的方法，如果忘记了就回去看看吧！

2 矩阵基础

在神经网络中，我们经常会用到矩阵，因为矩阵让数学式的表示更为简单，下面让我们来学习矩阵的知识吧。

2.1 矩阵

什么是矩阵呢？其实矩阵就是数字的阵列，如下所示 $$A=\left[ \begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix} \right] $$

横排称为行，竖排称为列。在上例中，矩阵由3行3列构成，称为3行3列的矩阵。

另外如上图所示，行数与列数相同的矩阵称为方阵。此外，如下图所示的矩阵$X$、 $Y$分别称为列向量、行向量，也可以简单地称为向量。 $$X=\left[ \begin{matrix} 3 \\ 1 \\ 4 \end{matrix} \right] ,Y=\left[ \begin{matrix} 2 & 7 & 1 \end{matrix} \right] $$

下面是$m$行$n$列的矩阵。位于第$i$行第$j$列的值（称为元素）用$a_{ij}$表示。 $$A=\left[ \begin{matrix} { a }_{ 11 } & { a }_{ 12 } & \cdots & { a }_{ 1n } \\ { a }_{ 21 } & { a }_{ 22 } & \cdots & { a }_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ { a }_{ m1 } & { a }_{ m2 } & \cdots & { a }_{ mn } \end{matrix} \right] $$

有一种有名的矩阵叫做单位矩阵，它是对角线上的元素都为1，其他元素都为0的方阵，通常用$E$表示。如下方所示是一个2阶和一个3阶的单位矩阵 $$E=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}，E=\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right] $$

2.2 矩阵相等

两个矩阵$A、B$相等的含义是它们对应的元素相等，记为$A=B$ 。

示例：当$A=\begin{bmatrix} 2 & 7 \\ 1 & 8 \end{bmatrix}，B=\begin{bmatrix} x & y \\ u & v \end{bmatrix}$时，如果$A=B$，则$x,y,u,v等于多少？$

答：$x=2,y=7,u=1,v=8$

2.3 矩阵的和、差、常数倍

矩阵的和和差的前置条件是，两个矩阵是相同大小的（形状相同，不是相等）

矩阵的和、差都很简单，就是同位置的元素进行加减，常数倍也是每个位置的元素进行倍数计算

示例：$A=\begin{bmatrix} 2 & 7 \\ 1 & 8 \end{bmatrix}，B=\begin{bmatrix} 2 & 8 \\ 1 & 3 \end{bmatrix}$，求他们的和、差和A的3倍 $$A+B=\begin{bmatrix} 2+2 & 7+8 \\ 1+1 & 8+3 \end{bmatrix}=\begin{bmatrix} 4 & 15 \\ 2 & 11 \end{bmatrix}$$ $$A-B=\begin{bmatrix} 2-2 & 7-8 \\ 1-1 & 8-3 \end{bmatrix}=\begin{bmatrix} 0 & -1 \\ 0 & 5 \end{bmatrix}$$ $$3A=\begin{bmatrix} 3\times 2 & 3\times 7 \\ 3\times 1 & 3\times 8 \end{bmatrix}=\begin{bmatrix} 6 & 21 \\ 3 & 24 \end{bmatrix}$$

2.4 矩阵的乘积

矩阵相乘的前置条件是，第一个矩阵的行数等于第二个矩阵的列数

矩阵的乘积是真的难算，经常绕一绕就进去了，同位置相乘的乘法我们会在后面讲

矩阵的乘积在神经网络的应用中特别重要。对于两个矩阵$A、B$，将$A$的第$i$行看作行向量，$B$的第$j$列看作列向量，将它们的内积作为第$i$行第$j$列元素，由此而产生的矩阵就是矩阵$A、B$的乘积$AB$。

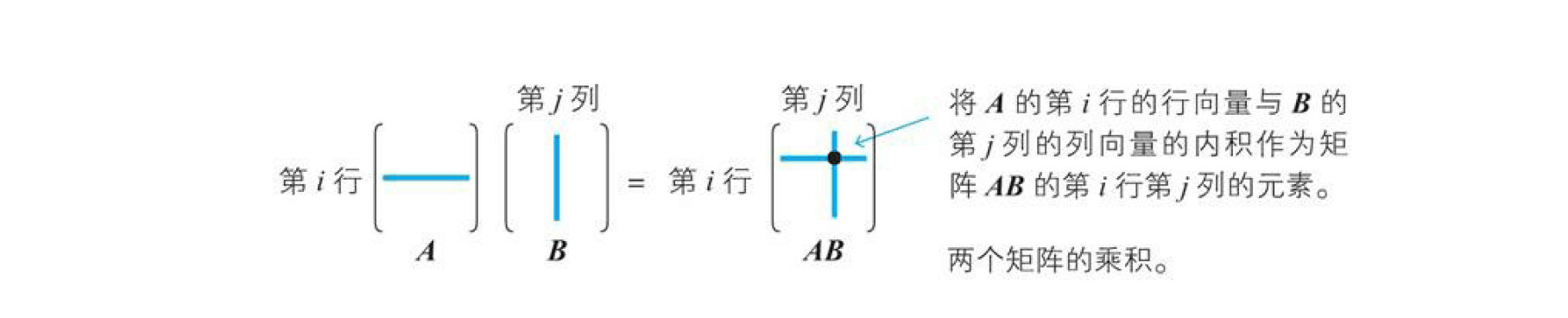
示例：$A=\begin{bmatrix} 2 & 7 \\ 1 & 8 \end{bmatrix}，B=\begin{bmatrix} 2 & 8 \\ 1 & 3 \end{bmatrix}$，求$AB和BA$ $$AB=\begin{bmatrix} 2 & 7 \\ 1 & 8 \end{bmatrix}\cdot \begin{bmatrix} 2 & 8 \\ 1 & 3 \end{bmatrix}=\begin{bmatrix} 2\times 2+7\times 1 & 2\times 8+7\times 3 \\ 1\times 2+8\times 1 & 1\times 8+8\times 3 \end{bmatrix}=\begin{bmatrix} 11 & 37 \\ 10 & 32 \end{bmatrix}$$ $$BA=\begin{bmatrix} 2 & 8 \\ 1 & 3 \end{bmatrix}\cdot \begin{bmatrix} 2 & 7 \\ 1 & 8 \end{bmatrix}=\begin{bmatrix} 2\times 2+8\times 1 & 2\times 7+8\times 8 \\ 1\times 2+3\times 1 & 1\times 7+3\times 8 \end{bmatrix}=\begin{bmatrix} 12 & 78 \\ 5 & 31 \end{bmatrix}$$

通过上面的示例，我们会发现矩阵的乘法步满足交换律，也就是说除例外情况，矩阵的乘法满足下方式子 $$AB\neq BA$$

然单位矩阵$E$与任意矩阵$A$的乘积都满足乘法交换律，如下所示 $$AE=EA=A$$

2.5 Hadamard乘积(哈达马积)

对于相同形状的矩阵$A、B$，将相同位置的元素相乘，由此产生的矩阵称为矩阵$A、B$的Hadamard乘积，用$A\bigodot B$表示

示例：$A=\begin{bmatrix} 2 & 7 \\ 1 & 8 \end{bmatrix}，B=\begin{bmatrix} 2 & 8 \\ 1 & 3 \end{bmatrix}$，求$A\bigodot B$ $$A\bigodot B=\begin{bmatrix} 2 & 7 \\ 1 & 8 \end{bmatrix}\cdot \begin{bmatrix} 2 & 8 \\ 1 & 3 \end{bmatrix}=\begin{bmatrix} 2\times 2 & 7\times 8 \\ 1\times 1 & 8\times 3 \end{bmatrix}=\begin{bmatrix} 4 & 56 \\ 1 & 24 \end{bmatrix}$$

2.6 转置矩阵

将矩阵$A$的第$i$行第$j$列的元素与第$j$行第$i$列的元素交换，由此产生的矩阵称为矩阵$A$的转置矩阵（transposed matrix），用 ${ }^{ t }{ A }、 { A }^{ t }$等表示。

示例1：$A=\begin{bmatrix} 2 & 7 \\ 1 & 8 \end{bmatrix}$，求${ }^{ t }{ A }$ $${ }^{ t }{ A }=\begin{bmatrix} 2 & 1 \\ 7 & 8 \end{bmatrix}$$

本文到此结束，下篇文章我们将进入导数的篇章啦！

深度学习数学基础(四)之线性代数基础