本篇内容含有大量公式,如果展示不佳,请跳转至原文
之前我们提过,说神经网络会很牛逼的自己学习,那这个自己学习是什么原理呢?如果用数学上的非人话就是对权重和偏置进行最优化,使输出符合学习数据,人话说就是不断的求导调整参数,让算法找到学习数据的规律。而对于这里的最优化,求导是不可缺少的一部分。
1 导数基础
1.1 导数的定义
导数就是函数图像在某一点处的斜率,比如下图,作出函数$f\left( x \right)$的图像,$f^{'}\left(x\right)$表示图像切线的斜率。因此光滑图像的函数是可导的。
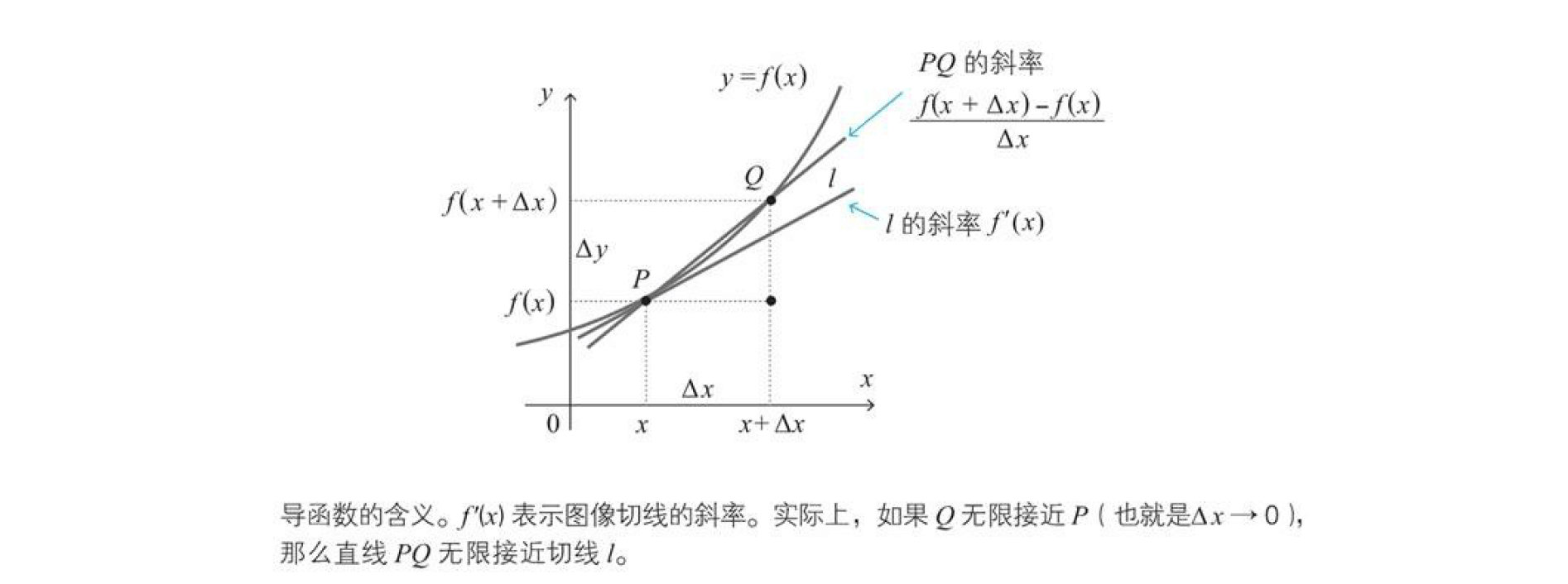
函数$f\left( x \right)$的导函数$f^{'}\left(x\right)$定义如下
$$f^{ ' }\left( x \right) =\lim _{ \Delta x\rightarrow 0 }{ \frac { f\left( x+\Delta x \right) -f\left( x \right) }{ \Delta x } } $$
注:$\Delta$读作 delta,对应拉丁字母 D。此外,带有 (prime)符号的函数或变量 表示导函数。
$\lim _{ \Delta x\rightarrow 0 }{ (\Delta x的式子) } $是指当$\Delta x$无线接近0时,$(\Delta x的式子)$接近的值,这个lim就是极限
示例 1:当$f(x)=3x$,它的$f`(x)$是多少? $$f'(x)=\lim _{ \Delta x\rightarrow 0 }{ \frac { 3(x+\Delta x)-3x }{ \Delta x } } =\lim _{ \Delta x\rightarrow 0 }{ \frac { 3\Delta x }{ \Delta x } } =\lim _{ \Delta x\rightarrow 0 }{ 3 } =3$$
示例 2:当$f(x)=x^2$,它的$f`(x)$是多少? $$f'(x)=\lim _{ \Delta x\rightarrow 0 }{ \frac { { (x+\Delta x) }^{ 2 }-x^{ 2 } }{ \Delta x } } =\lim _{ \Delta x\rightarrow 0 }{ \frac { 2x\Delta x+{ (\Delta x) }^{ 2 } }{ \Delta x } } =\lim _{ \Delta x\rightarrow 0 }{ (2x+\Delta x) } =2x$$
如上示例,已知函数$f(x)$,求导函数$f'(x)$,称为对函数$f(x)$求导,当$f'(x)$存在时,称函数可导
1.2 常用导数公式
在神经网络中,我们会经常用到导数,下面就简单列举几个常用的导数公式。 $$( c )'=0,c代表常数$$ $$(x)'=1$$ $$(x^2)'=2x$$ $$(e^x)'=e^x$$ $$({e}^{-x})'=-{e}^{-x}$$
1.3 导数符号
在本文的1.1中的公式中,函数$f\left( x \right)$的导函数用$f^{'}\left(x\right)$表示,但是也存在不同的表示方式,比如下面使用分数表示的方法 $$f^{ ' }\left( x \right) =\frac { dy }{ dx } $$
这种表示方式是十分方便的,因为复杂的函数可以像分数一样计算导数
示例1:$( c )'=0$,可以记为$\frac { dc }{ dx } =0$(c为常数)
示例2:$( x )'=1$,可以记为$\frac { dx }{ dx } =1$
1.4 导数的线性性质
我们在计算中免不了使用加减乘除,在这里我们先介绍导数的线性性,其实就是导数的加减法和常数倍,而这个导数的线性性就是我们后面会说到的误差反向传播算法背后的主角
1.4.1 导数的加减法
和的导数等于导数的和
$${f(x)+g(x)}’=f'(x)+g'(x)$$
差的导数等于导数的差
$${f(x)-g(x)}’=f'(x)-g'(x)$$
1.4.2 导数的常数倍
常数倍的导数为导数的常数倍
$${cf(x)}'=cf'(x)$$
示例:$C={(2-y)}^{2}$,(y为变量)时,求$C'$ $$C'=(4-4y+y^2)'\\=(4)'-4(y)'+({y}^{2})'\\=0-4+2y=2y-4$$
1.5 分数函数导数
当函数是分数形式时,求导时可以使用下面的分数函数的求导公式。$f(x)$不能取0 $$\left\{ \frac { 1 }{ f(x) } \right\}'=-\frac { f'(x) }{ { \left\{ f(x) \right\} }^{ 2 } }$$
1.5.1 sigmoid函数的导数
sigmoid函数$\sigma (x)$是神经网络中最著名的激活函数之一,我们之前有讲过,它的定义如下: $$\sigma (x)=\frac { 1 }{ 1+{ e }^{ -x } }$$
在后面的梯度下降算法中,需要对这个函数求导,求导时我们使用下面的公式会更方便一些,通过这个式子及时不对sigmoid函数求导,也能通过$\sigma (x)$的值得到sigmoid函数的导函数值
$$\sigma ‘(x)=\sigma(x)(1-\sigma(x))$$
1.5 最小值的条件
上面我们说过由于导函数$f’(x)$表示切线的斜率,那么我们就可以得到在后面最优化中需要用到的一条极其重要的原理,该原理如下所示 $$当函数f(x)在x=a处取得最小值时,f'(a)=0$$
证明:导函数$f'(a)$表示切线斜率,所以根据下图可以清楚地看出$f'(a)=0$。
在使用时要一定要记住下面的条件 $$f'(a)=0是函数f(x)在x=a处取最小值的必要条件$$
从下面的函数$y=f(x)$的图像可以清楚地看出这一点。
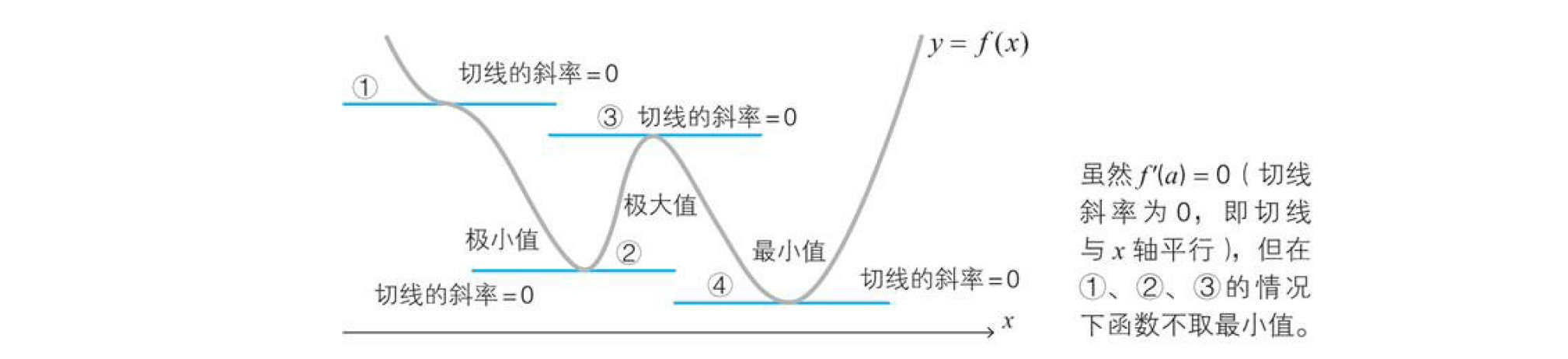
所以我们就看到以下必要不充分的条件:
$$f(x)最小\Rightarrow f'(a)=0\\ f(x)最小\nLeftarrow f'(a)=0$$
就是因为这个性质,导致我们后面在使用梯度下降算法时,遭遇到了很大的困难
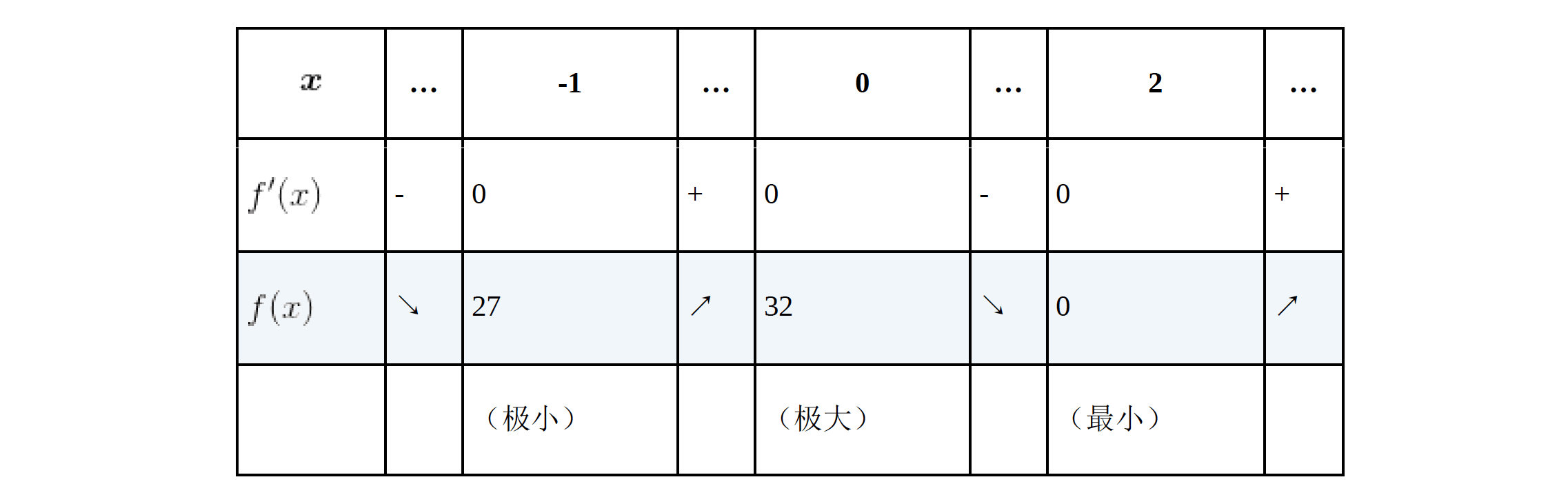
示例:求$f(x)=3x^4-4x^3-12x^2+32$的最小值
首先我们求出该函数的导函数$f'(x)=12x^3-12x^2-24x=12x(x+1)(x-2)$
下面是该函数的增减表,我们发现在$x=-1、0、2$的时候,该函数的导函数为0,但是$x=-1、0$时却不是最小值,所以验证了我们上方所说的性质
2 偏导数基础
上面我们所说的导数都是基于一元的函数,那么多元的函数怎么办呢?其实多元函数也可以进行求导,只不过我们必须指明要对哪个一个变量进行求导,而关于某个特定的变量的导数就叫偏导数。
2.1 偏导数的定义
多元函数进行求偏导时,除了指定的变量外其他的变量都作为常数来求导,比如有个二元函数$z=f(x,y)$,我们对它的变量x进行求导,以此求得的导数称为关于x的偏导数,用下方的符号来进行表示
$$\frac { \partial z }{ \partial x } =\frac { \partial f(x,y) }{ \partial x } =\lim _{ \Delta x\rightarrow 0 }{ \frac { f(x+\Delta x,y)-f(x,y) }{ \Delta x } } $$
关于y的偏导数,也差不多 $$\frac { \partial z }{ \partial y } =\frac { \partial f(x,y) }{ \partial y } =\lim _{ \Delta x\rightarrow 0 }{ \frac { f(x,y+\Delta y)-f(x,y) }{ \Delta y } } $$
示例:当$z=wx+b$时,$\frac { \partial z }{ \partial x } =w,\frac { \partial z }{ \partial w } =x,\frac { \partial z }{ \partial b } =1$
2.2 多变量函数的最小值条件
之前我们说过,光滑的单变量函数$y=f(x)$在点$x$处取得最小值的必要条件是导函数在该点取值0,这个性质在多元函数同样适用,例如对两个变量的函数,可以如下所示。 $$函数z=f(x)取得最小值的必要条件是\frac { \partial f }{ \partial x } =0,\frac { \partial f }{ \partial y }=0$$
上面的性质很容易扩展到$n$个变量的情形,只要满足所有偏导数都为0,此外,从下图可以清楚地看出上述的条件是成立的。因为从$x$方向以及$y$方向来看,函数$z=f(x,y)$取得最小值的点就像葡萄酒杯的底部。
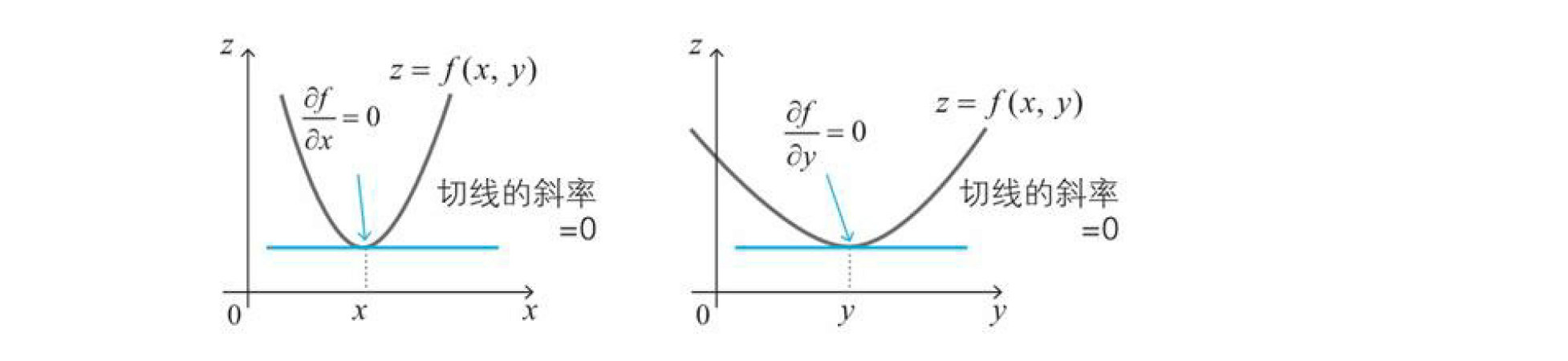
但是要记住的是上面的条件跟单变量函数的最小值条件一样,即使满足上述条件,也不能满足在该点取得最小值。
2.3 拉格朗日乘数法
在实际的最小值问题中,有时会对变量附加约束条件,例如下面这个问题
示例:当$x^2+y^2=1$时,求$x+y$的最小值
这种情况下我们使用
拉格朗日乘数法,首先引入参数$\lambda $,创建下面的函数$L$ $$L=f(x,y)-\lambda g(x,y)=(x+y)-\lambda(x^2+y^2-1)$$ $$\frac { \partial L }{ \partial x } =1-2\lambda x=0$$ $$\frac { \partial L }{ \partial y } =1-2\lambda y=0$$ 根据这些式子以及约束条件$x^2+y^2=1$,可得x=y=$\lambda=\pm \frac { 1 }{ \sqrt { 2 } } $因此,当$x=y=-\frac { 1 }{ \sqrt { 2 }}$时,$x+y$取最小值$-\sqrt { 2 }$
在用于求性能良好的神经网络的正则化技术中,经常会使用该方法。